三 平方 の 定理 簡単 な 解き方 三平方の定理を使うと直角三角形の 2 つの辺の長さからもう一つの辺の長さを求めることができます このページでは三平方の定理を分かりやすく説明しています中学校で学習する前の人にも三平方の定理の意味を理解して a, b, c a,b,c a,b,c はいずれも奇数となり, a = 2 A 1, b = 2 B 1, c = 2 C 1 a=2A1,b=2B1,c=2C1 a = 2A1,b = 2B 1,c = 2C 1 とおける( A, B, C A,B,C A,B,C は非負整数)。 このとき, 8 n 3 = ( 2 A 1) 2 ( 2 B 1) 2 ( 2 C 1) 2 8n3= (2A1)^2 (2B1)^2 (2C1)^2 8n3 = (2A1)2 (2B 1)2 (2C 1)2特集 生徒が喜ぶ「三平方の定理」の授業 提言・「三平方の定理」は面白い教材 この教材を有効に生かすために ・・・・・・ 上垣 渉;

円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト
三 平方 の 定理 小学生
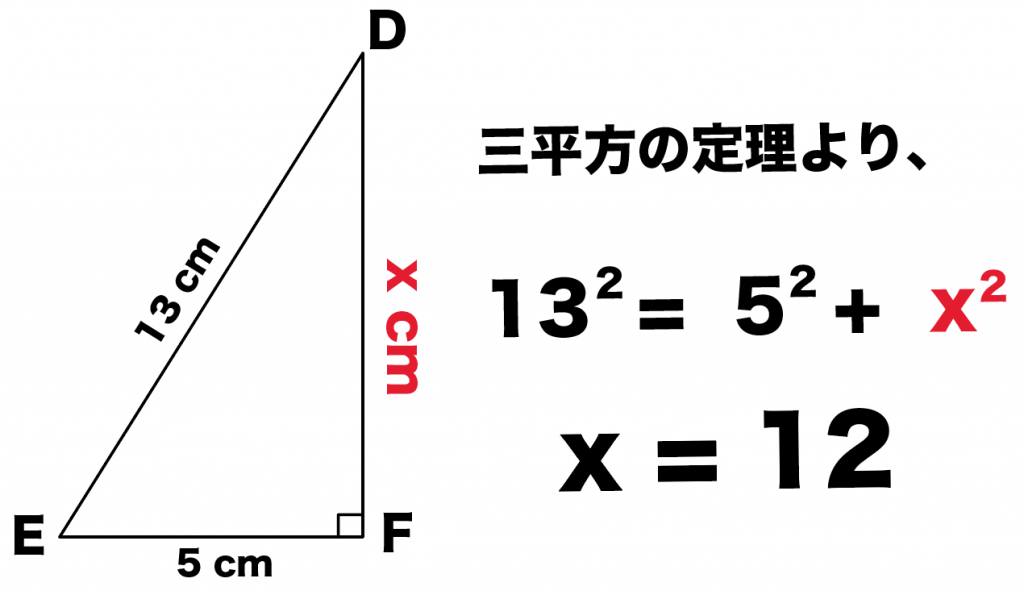
三 平方 の 定理 小学生-3 小学生が導き出す 手助け問題 31 (1) 三角形abcの面積;A 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.) これを用いて3辺の長さのうち2辺の長さが分かっているとき,残りの1辺の長さを求めることができます. 証明 ・・・ 証明の仕方は何十通り~何百通りあると言われています。 中でも簡単そうなのは次の証明です。 《問題1》 次の直角三角形において,xの長さを求めなさい (1)
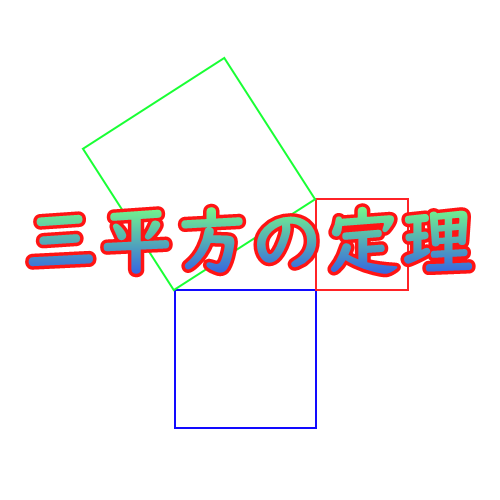



三平方の定理がひと目で分かる展示が面白い アロエのおうち
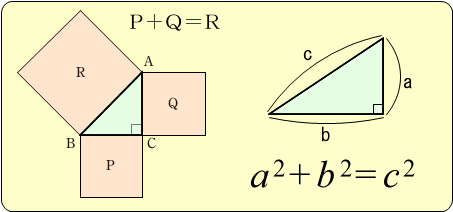
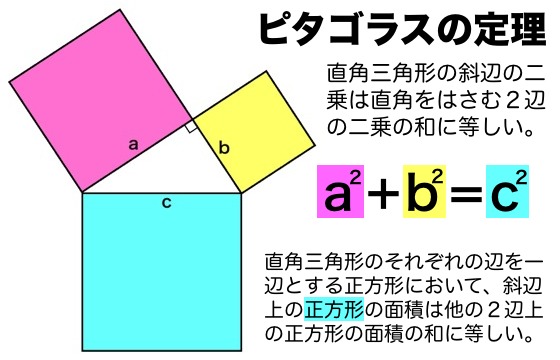
三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるの2 大人向け ピタゴラゴラスの定理の証明 21 面積図を使った証明;見渡せる距離をx ㎞とすると,三平方の定理より x 2+637 =(6378+3776)2 これを解いてx を求めると, x =2195 約2㎞見渡せる。 図 (省略) 相似な図形の面積と体積 日常生活の場面で対 象を理想化や単純化 することで相似な図 形と見なし,相似な
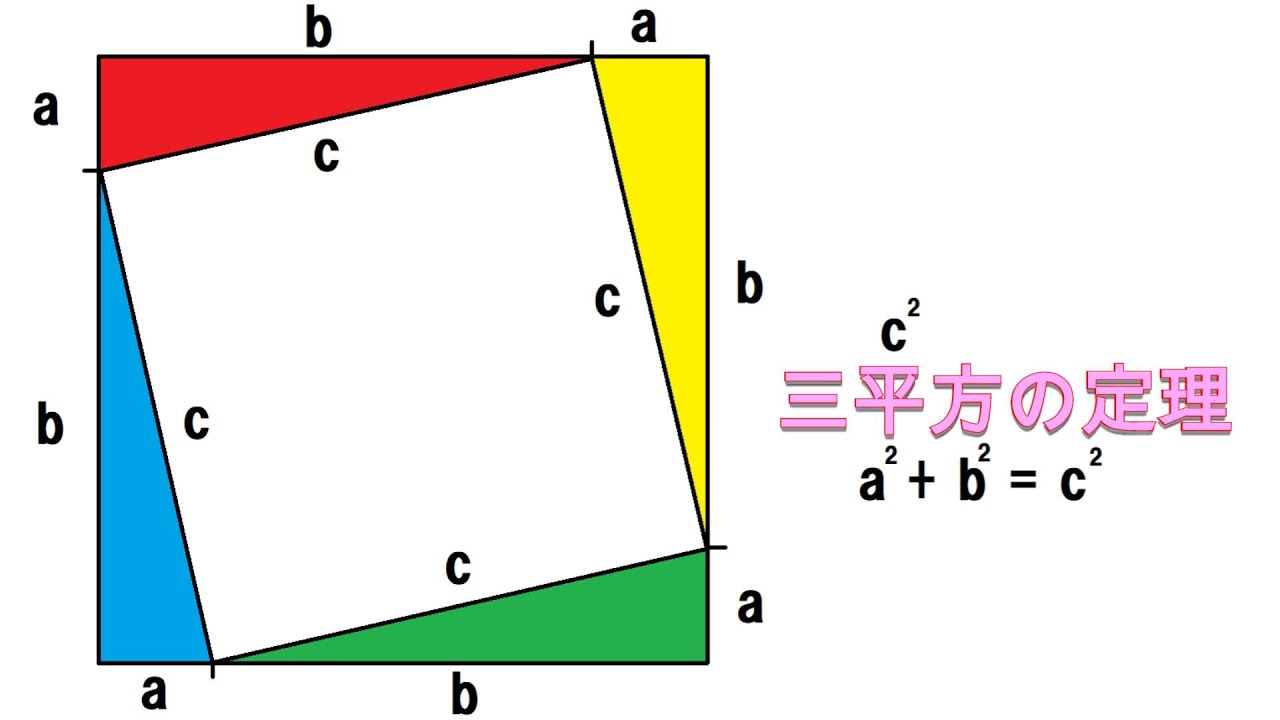
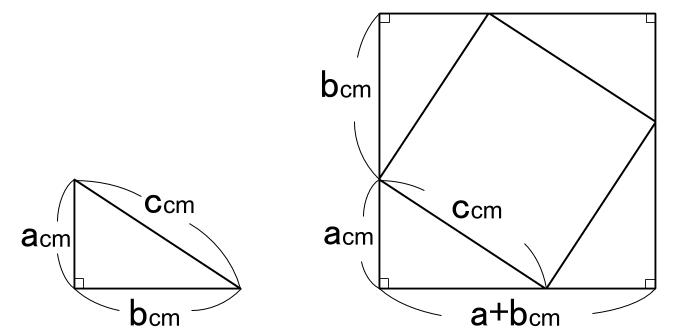
中学3年生 数学 平方根の加法・減法 問題プリント 無料ダウンロード・印刷 √の中が等しい数は、文字式の同類項と同じように分配法則を使ってまとめることができることなどについて理解し、平方根の加法・減法を練習する問題プリントです。1.三平方の定理って何? みなさんは、中学生の時に 三平方の定理 を勉強したと思いますが何をするものだったのか覚えていますか? 三平方の定理とは、直角三角形の3つの辺の長さの関係を表す公式のことです。 三平方の定理の公式はどのような時に使われるのかというと、図形の辺の長さの計算です。 三平方の定理は別名ではピタゴラスの定理ともいわれてい最後は、問題も用意しているので、この記事を通して三平方の定理の逆について理解を深めていきましょう! 三平方の定理の証明 AB=c, BC=a, AC=b, ∠ACB=90°の直角三角形ABCと合同な直角三角形を図のように並べる。 このときa 2 b 2 =c 2 となることを次のように証明した。 空欄ア、イに適切な文字または数字を入れよ。 Error 三 平方 の 定理 証明 中学生" /> 三平方の定理
三 平方 の 定理 直角 三角形 Pictngamukjp5mhn 直角三角形において、「直角」をはさむ2つの辺の長さを \ (a,b\)、斜辺の長さを \ (c\) としたとき 三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵|アタリマエ!3この定理の逆も成り立つ。すなわち、三角形の1辺の平方が他の2辺の平方の和に等しければ、始めの辺に対する頂角は直角である。この逆定理の成立によって、たとえば、辺の長さが3、4、5である三角形は3 2 +4 2 =5 2 であるから、直角三角形となる。この3三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し



小学生でも分かる三平方の定理 Pythagoras Theorem Youtube




世界一わかりやすい数学問題集中3 7章 三平方の定理
从 1730 年至 1770 年, 在大约四十年的时间里 Euler 证明了许多与四平方定理有关的结果, 为后来这一定理的证明创造了条件, 但他本人却很遗憾地未能率先证明这一定理 注三 。 1770 年, 法国数学家 Joseph Lagrange () 以 Euler 的一个结果为基础, 率先给出了 中学受験算数 三平方 ピタゴラス の定理を小学生向けに証明 中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と 中3数学 三平方の定理 で最も重要なポイントとは 映像授業の 円に関する定理を集めてみた。五角形と円、六角形と円・・・ ここには何か関連がありそう。4点以上が円周上にあることの不思議。 ・・・ やってみてわかってきたこと (1)二つの円で偶数個の円を描くとぴったり一致すること (2)偶数個の円の中心は楕円の外接多角形であること (3)その楕円の




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より
二次元での定理を三次元に拡張 1. はじめに 直角三角形で成り立つ三平方の定理(ピタゴラスの定理)というのはかなり有名です。 私たちはこの定理を三次元(立体)に拡張したときにどうなるのかというのに興味を持ち ました。数学史から入る「三平方の定理」 「三平方の定理」は,いつ,どのようにして発見されたか ・・・・・・ 片野 善一郎三 平方 の 定理 表 数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo ソフト ボール 投げ 小学生




三平方の定理を使わず面積を求める が小学生向けの問題だったとはね Ts0818のブログ



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs
三 平方 の 定理 証明 種類 小学生でも分かるようにピタゴラスの定理を証明する方法を紹介します。ぜひお子さんとやってみて下さい ピタゴラスの定理の覚え方としては、 斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 となります。 となります。 が成り立ちます。 これを「三平方の定理」 といいます。平方根が出てくる場合が多いので、平方根の計算も同時に覚えましょう。 斜辺以外の一辺の長さを求める場合は、三平方の定理を式変形して a² = c² – b² = (cb)(cb)




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
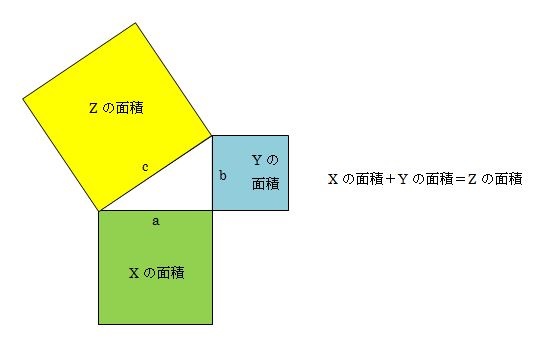



三平方の定理 もう一度やり直しの算数 数学
ピタゴラスの定理の覚え方としては、 斜辺の平方は他の2辺の平方の和 が最も優れているだろう。 昨今の生徒の意識として、結果さえ覚えればOKで、その成り立ち等に関心を払わない 場合が多い。四平方和定理 (英语:Lagrange's foursquare theorem) 说明每个正整数均可表示为4个整数的平方和。 它是费马多边形数定理和华林问题的特例。 注意有些整数不可表示为3个整数的平方和,例如7。 解答 下の図のように補助線をひき、左の直角三角形に 三平方の定理を用います。 x2 = 22 x 2 = 2 2 8 2 x2 = 68 x 2 = 68 x = ±√68 x = ± 68 = ±2√17 = ± 2 17 この問題では、当然 x x は正の値なので x = 2√17 x = 2 17



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ
a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじいサイトがあります。 →Pythagorean Theorem 105個の中で,個人的に「簡単で美しい」と思った証明を4つ(#3,6,42,47)ほど紹介します。 目次 正方形を用いた証明 相似を用いた三平方の定理をご存知でしょうか? ピタゴラスの定理と言った方がピンとくるかもしれません。 これは、直角三角形の二辺の長さが分かっていれば、残りの一辺の長さを求めることが出来るものです。 辺bの長さを求める b = √ (a2 c2) 辺aの長さを求めるピタゴラスの定理(3平方の定理)とは ピタゴラスの定理っていうのは、 直角三角形の3辺の長さの関係を表したものだよ その関係っていうのは、$斜辺^2=底辺^2高さ^2$だよ 辺の長さを求める時は、この式に当てはめることで求めることが 三平方の定理の証明!




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ
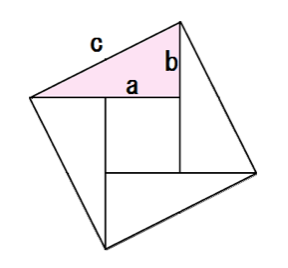



中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく
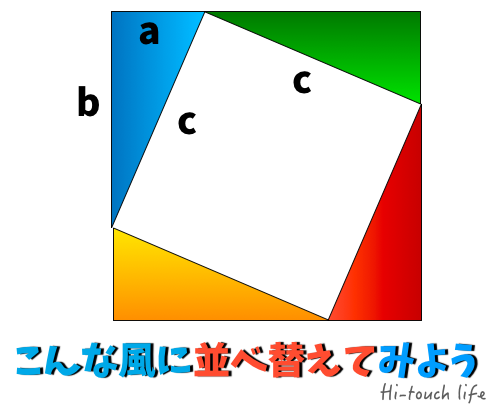
この図からどのようにして三平方の定理が 導き出されるのだろうか。 ウモクホ数学に匹敵する学問体系を築き上げた 古代中国の学者に思いをはせながら、 証明方沵を考えてみてください。 14....補足2 三平方の定理の三次元拡張知育・学習プリント 無料ダウンロード 幼児教材・知育プリント ひらがな練習、数、間違い探し、迷路、ぬりえ、点つなぎ、時計など。 ちびむすドリル 幼児 小学生の学習プリント 算数プリント、漢字練習プリント、ローマ字、ます計算、白地図など三平方の定理の証明と使い方 三平方の定理 とは、 直角三角形の直角をはさむ2辺の長さを a, b, 斜辺の長さを c としたときに、 公式 a2 b2 = c2 が成り立つ という定理です。 ここで、斜辺とは、直角三角形の直角に対する対辺のことです。 三平方の定理は、別名、 ピタゴラスの定理 とも呼ばれます。 三平方の定理(ピタゴラスの定理) 3 辺の長さが a, b, c の直角




小学生の三平方の定理 生きる力を育む ysゼミナールと保護者の交流の場 Encafe



数の不思議 奇数の和でできるピタゴラス数 Note Board
平方根 平方根(1) 問題一括 (8,085Kb) 解答一括 (9,324Kb) 平方根(2) 平方根の大小 有理数と無理数 平方根の乗法 平方根の除法 平方根の性質(1) 平方根の性質(2) 平方根の近似値 根号を含む計算 有理化 平方根の加法・減法(1) 平方根の加法・減法(2) 平方根の三平方の定理に当てはめる。 x 2 1 2 =3 2 x 2 =91 x 2 =8 x=±2 2 x>0よりx=2 2 答 2 2 cm 確認次のそれぞれの三角形で、頂点Aから辺BCにおろした垂線の長さを求めよ。 答表示 1辺8cmの正三角形 A B C 4 3 cm AB=AC=29cm, BC=40cmの二等辺三角形 A B C 21cm




75 三 平方 の 定理 証明 中学生 最高のぬりえ




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




中学生 三平方の定理の利用のノート一覧 Clear




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




75 三 平方 の 定理 証明 中学生 最高のぬりえ



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



かなり難しい中学受験の算数の問題です 問題文と図は写真の通りですが 小学生が対 Yahoo 知恵袋




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




75 三 平方 の 定理 証明 中学生 最高のぬりえ
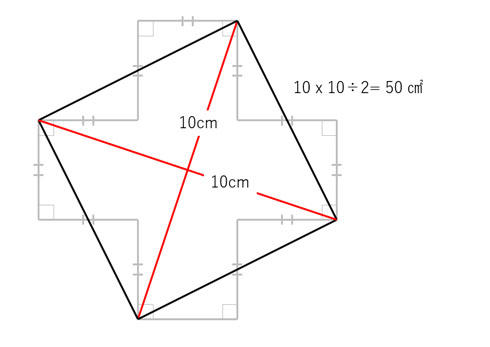



この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ



無料でダウンロード ピタゴラス の 定理 小学生
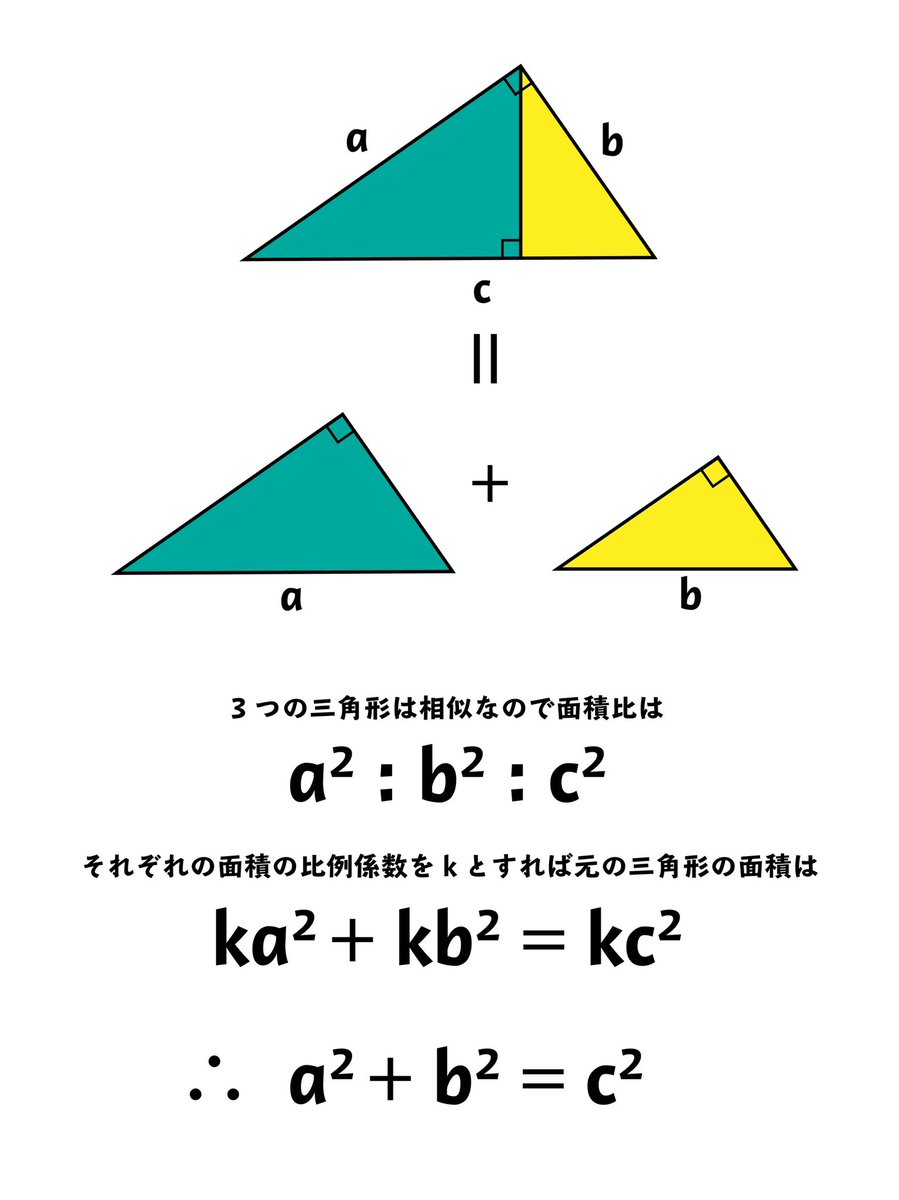



ヨビノリやす アインシュタインが小学生のときに見つけた三平方の定理の証明



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




算数の問題 四角形abcdの面積を求める問題です これを三平方の定理を 小学校 教えて Goo




にしはら学習塾 今日の中学受験算数 21 6 25 中学受験している小学生 三平方の定理まで学習してる中3生 解いてみましょう 答え合わせは塾長の西原まで さいたま市大宮区櫛引町の個人塾 にしはら学習塾




無料でダウンロード ピタゴラス の 定理 小学生




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



これなら小学生でも分かる 水で車輪を使って ピタゴラスの定理 を証明する実験動画 コモンポストムービー




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



ピタゴラスの定理 の思いで チャンネルf



質問にお答えします 小学生でもわかる数学とは 教育研究所arcs




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



1



面積の問題 小学生 中学生 三平方の定理 みんなの算数クラブ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三平方の定理 小学生に分かるはずがない アニメーションへのボケ ボケて Bokete




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
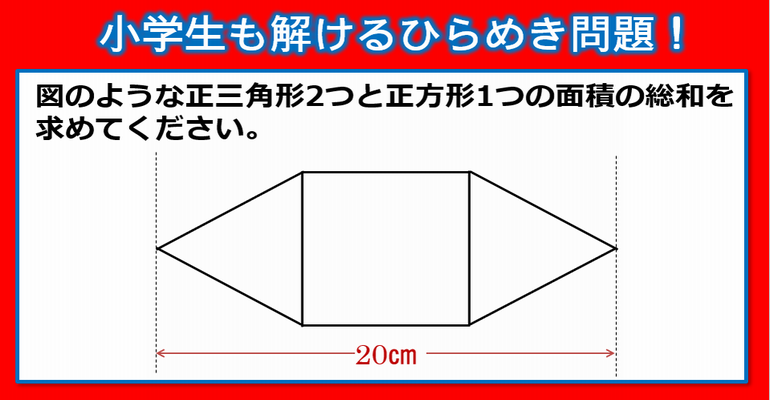



ひらめき算数 小学生も解ける 美しい良問 ネタファクト




中学生 三平方の定理のノート一覧 Clear




中学生 三平方の定理のノート一覧 Clear




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




新鮮なピタゴラス の 定理 小学生 子供のための最高のぬりえ




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




ピタゴラスの定理の証明に挑戦する小学生 モンテッソーリ教育 ピタゴラスの定理 モンテッソーリ教育 モンテッソーリ




中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su




ヒポクラテスの定理は三平方の定理を知っていたら覚える必要なし 勉強法全般




三平方の定理 高さの求め方編 中3 中学 数学 Youtube




新鮮なピタゴラス の 定理 小学生 子供のための最高のぬりえ



1
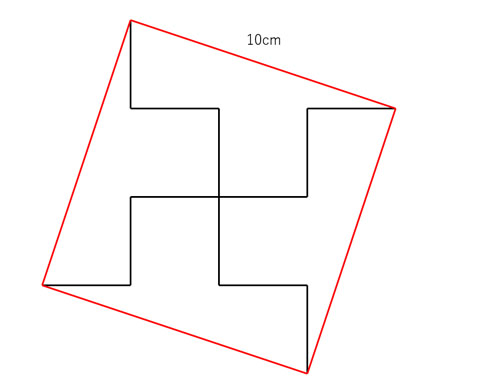



この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ



三平方の定理 小学生バージョンの解き方 江戸川女子中 09年 算数解法の極意




世界一わかりやすい数学問題集中3 7章 三平方の定理



図形 角度 面積問題 三平方の定理 中学生 練習問題45 60 75 3 4 5 の三角形 みんなの算数クラブ
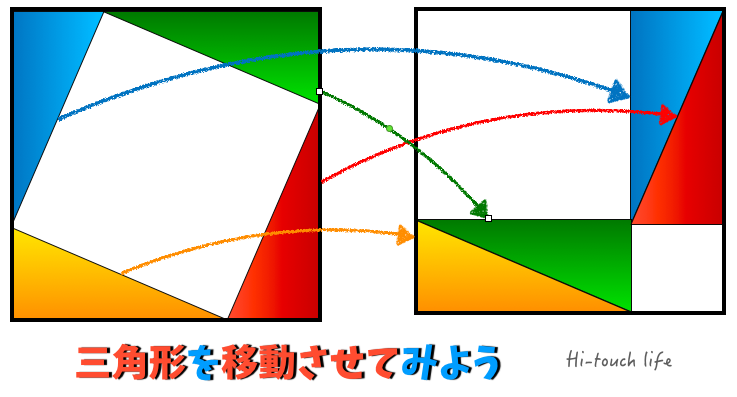



小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ




三平方の定理がひと目で分かる展示が面白い アロエのおうち
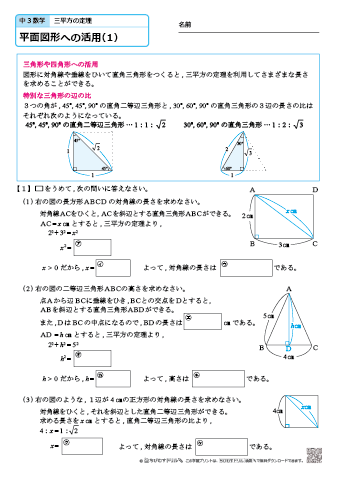



中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生



1




図形問題 小学生でもできる 三平方の定理なしで解く Youtube




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




中3数学 2分でわかる 三平方の定理の逆 Qikeru 学びを楽しくわかりやすく




小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ




算数の問題 四角形abcdの面積を求める問題です これを三平方の定理を 小学校 教えて Goo



図形 角度問題 三平方の定理 中学生 練習問題45 60 75 3 4 5 の三角形 みんなの算数クラブ
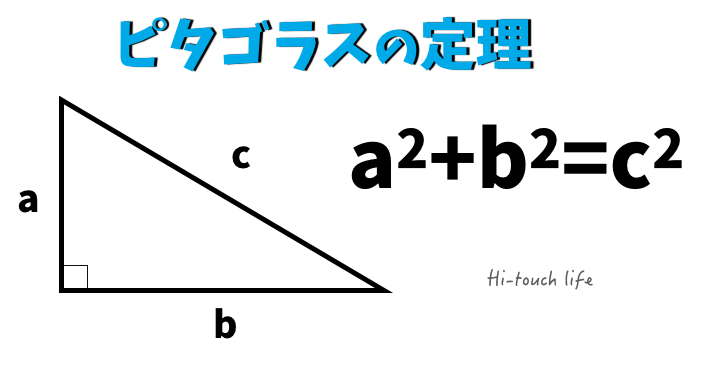



小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ
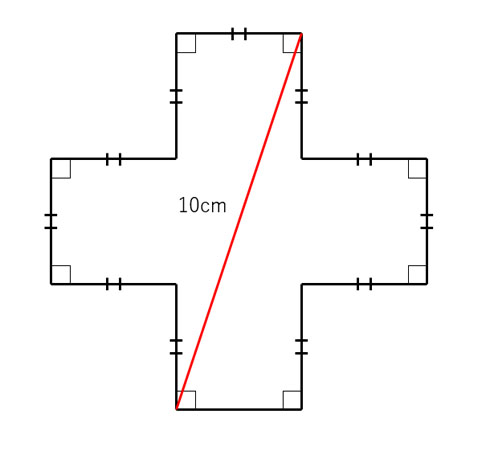



この図形の面積 三平方の定理を使わずに出せる ヒラメキで解く 算数 がちょっと手ごわい ねとらぼ
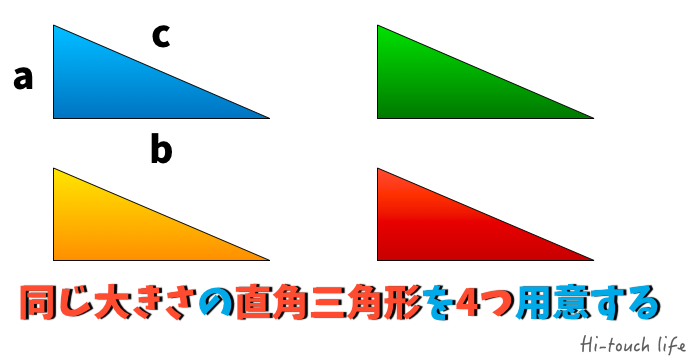



小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ



中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su




世界一わかりやすい数学問題集中3 7章 三平方の定理




数学 中3 61 三平方の定理 基本編 Youtube




中学受験算数で三平方の定理は使っていいのか ワイズナビ



三平方の定理や平方根を使わずに小学生が解く方法をご教示ください Yahoo 知恵袋



1




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ



小学生でもできるピタゴラスの定理の証明方法 算数 数学 理系思考を応援 Fireムーブメントを日本で実践するブログ




中学生でもわかる 三平方の定理 ピタゴラスの定理 の公式の4つの証明 Qikeru 学びを楽しくわかりやすく



小学生でも分かる三平方の定理 Pythagoras Theorem Youtube




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ




三平方の定理を証明せよ 中学生課題 ふるやまんのマスラボ奮闘記




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ
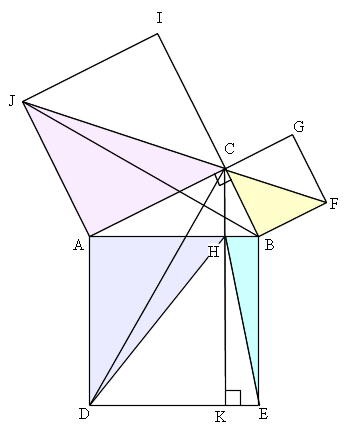



Mathematics 三平方の定理 1 三平方の定理の証明 働きアリ




ピタゴラス数 三平方の定理 整数解の求め方 質問への返答 Youtube




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学



無料でダウンロード ピタゴラス の 定理 小学生



面積の問題 小学生 中学生 三平方の定理の証明 みんなの算数クラブ



余弦定理も三平方の定理も知らない小学生でも理解できる解法はあるでしょうか Yahoo 知恵袋




新鮮なピタゴラス の 定理 小学生 子供のための最高のぬりえ




中学数学 ひもの長さが最短になるのはどんなとき 数スタ




小学生の三平方の定理 生きる力を育む ysゼミナールと保護者の交流の場 Encafe




三平方の定理 の作図 算数の種まき 理系ママの家庭学習 家庭保育園からピグマリオンへ カホっ子の小学校受験と中学受験




無料でダウンロード ピタゴラス の 定理 小学生
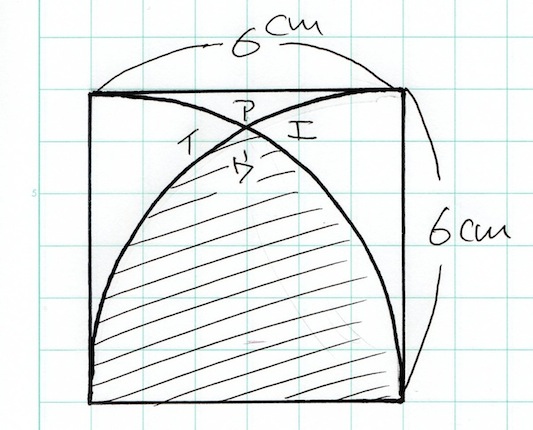



超難問 ねこたさんのごった煮日和



三平方の定理 小学生バージョンの解き方 江戸川女子中 09年 算数解法の極意




小学生でも三平方の定理 これ 知っ得 模索中の備忘録 馬耳東風馬の耳に念仏理系男子 10年生 の家庭学習




無料でダウンロード ピタゴラス の 定理 小学生


