Tenemos los valores exactos de 15°, 30°, 45°, 60° y 75° Hay que notar que para el ángulo de 75°, puede ser generado por la suma de 30° más 45° Ahora, habría que preguntarse si existe otro ángulo (comprendido dentro del primer cuadrante) que genere un valor exacto para las funciones seno y coseno aparte de los ya conocidos hasta ahora Ese ángulo existe y es lo que vamos aK El triangulo notable de 45 y 45 53 3K El triangulo de 37 y 53 1K K50 7K El triangulo de 8 y 30 K 3 74 2K 25K 7K 16 60 1K El triangulo de 30 y 60 24K El triangulo de 16 y 74 10K 37/2 3K El triangulo de 37/2 75 4K 5 K (6 2)K K 15 53/2 (6 2)K 2K El triangulo de 15 y 75 El triangulo de 53/2 67 5K 13K 23 12K El triangulo de 23 y 67 50 62 17K K61 8K 5KUn palo vertical de 1,75 m proyecta una sombra de 2 mSi la sombra de un edificio el mismo día,en el mismo sitio y a la misma hora mide 24 m,¿cuánto mide de alto el edificio?
1
Triángulo notable de 15 y 75 grados
Triángulo notable de 15 y 75 grados- Triángulos Notables Son aquellos triángulos que a partir de la razón de dos de sus lados se pueden calcular su tercer lado y la medida de sus ángulos internos Sólo existen dos triángulos rectángulos notables de medidas exactas y son aquellos que se deducen del triángulo equilátero y del cuadrado, estos son los de 30°, 60° y de 45°Triángulo rectángulo de 15 y 75 grados, ayuda como lo resuelvo anyelo está esperando tu ayuda Añade tu respuesta y gana puntos Nuevas preguntas de Matemáticas busco nov1a de 13 años doy coronita znoniduvygdyvudbycydguvd si;P(X;Y)=RAIZ CUADRADA DE 3 Xa Ybraiz de 7 entre 7 xelevado ala a 5y7yb7 1 el doble de un numero disminuido en siete unidades 2 la cuarta parte de




Perimetro De Un Triangulo Rectangulo
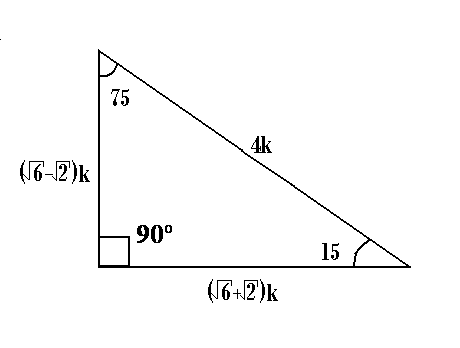
De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras que posee Más triángulos notables Triángulo notable de 37/2 grados Triángulo notable de 53/2 grados RazonesNotableNotebooks entrega los pedidos al servicio de mensajería en un plazo máximo de 24 horas durante los días laborables (excluidos fines de semana y festivos) tras confirmación del pago del pedido por parte del cliente No nos responsabilizamos de las posibles demoras de entrega causadas por el servicios de mensajería No obstante estamos aquí para ayudar a resolverTriángulo Notable de 15° y 75° Explicación de cómo formar el Triángulo Notable de 15° y 75°http//profesorajesuscomMáster Jesús Méndez CollantesFacebook
Educación 7022 visualizaciones 30 de abr de 13 Recomendar Recomendado Compartir Resolviendo triángulos TRIANGULO NOTABLE DE 15º Y 75º DEMOSTRACION TRIANGULO NOTABLE DE 15º Y 75º DEMOSTRACION Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't beginSe denomina triángulo notable a todo triángulo cuyos lados sean conocidos En la mayoría de
BC = 24 cm y A'B' = 15 cm,halla la longitud del segmento B'C'¿Qué teorema has aplicado? Observando el problema, nos damos cuenta que el Triángulo ABC es un Triangulo Rectángulo, Por ende pasaremos a completar el ángulo que le falta ( 75°) Luego de haber hecho esto nos llevaremos la gran sorpresa que los Triángulos Rectángulos AHB y BHM son iguales ya que tienen un lado en común ( BH ) y dos ángulos iguales ( 15° y 75 ° )Triángulo notable de 15° y 75° Podemos caracterizar a un triángulo como notable cuando existe una relación conocida entre sus lados En la mayoría de los casos, las relaciones entre sus lados se limitan a número enteros o número




Altura De Un Triangulo




Puntos Y Rectas Notables Del Triangulo Matematicascercanas
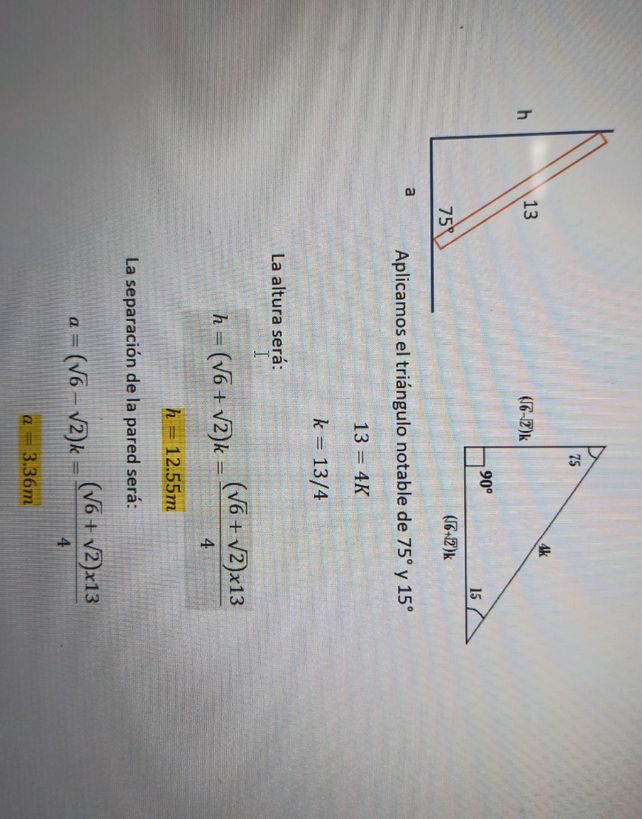
Calculamos CO=x, En elEs 48C notable de 15* y 75%, por teorema, AC=4(8H), entonces 8=4(BH), BH=2 Luego por el teorema de la bisectriz (28) se cumple que x=2 APROXIMADOS Triángulo notable de 37* y 53" En el 548€ notable de 30% y 60%, AC=2(4B), AC=4 Se observa que m La rampa tiene una longitud aproximada de 5,76 m para un ángulo de 15° Explicación paso a paso 1 representación gráfica de la rampa 2 triángulo notable de 15 y 75° Relaciono las longitudes de los lados de ambos triángulos En 2, calculo el valor de la constante k 1,5 m = k (√6 – √2) 1,5 m = k (2,45 – 1,41) 1,5 m = k (1,04) Triángulo notable de 54° y 36° Razones trigonométricas de los triángulos notables Triángulo notable de 75° y 15° Otros Triángulos Notables ¿Qué es un triangulo notable?
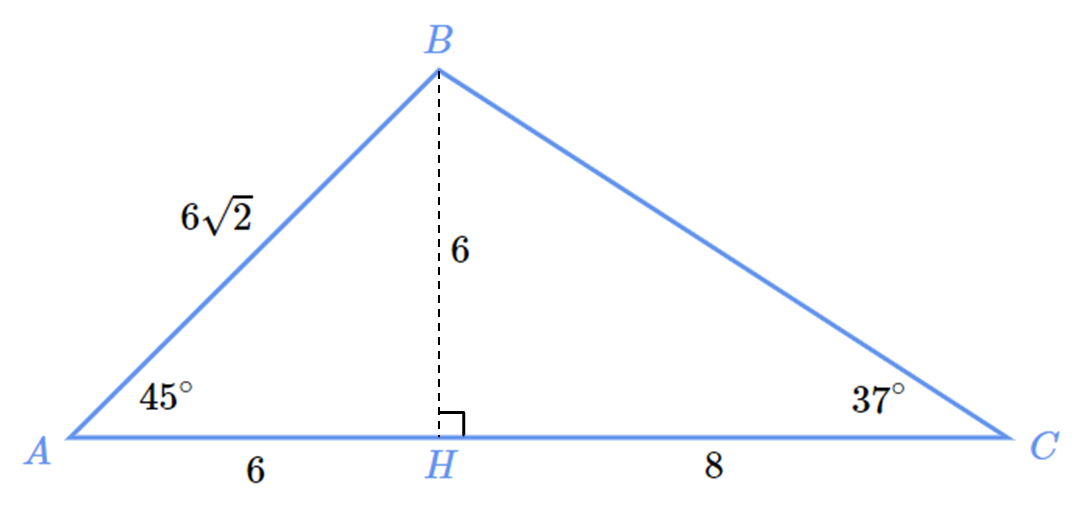



Problemas Sobre Razones Trigonometricas Notables De Angulos Agudos En Triangulos Rectangulos Articulo Khan Academy
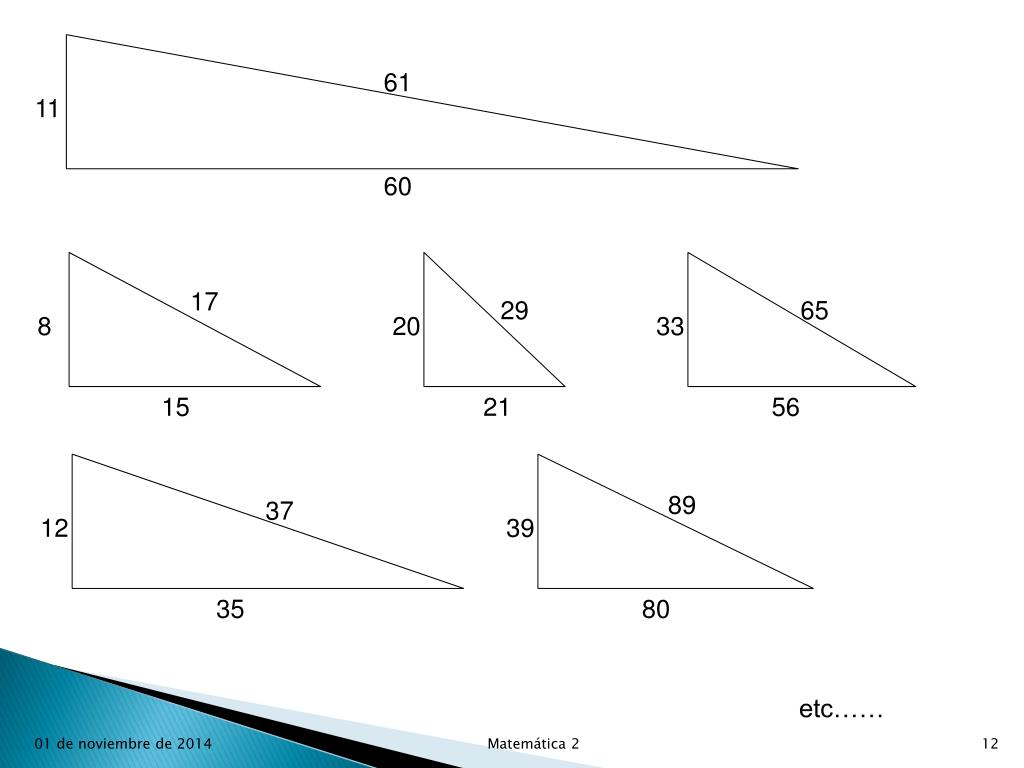



Ppt Matematica 2 Epe Powerpoint Presentation Free Download Id
A) 60°, 80° y 100° b) 40°, 60° y 80° c) 30°, 40° y 50° d) 45°, 60° y 75° e) 36°, 48° y 60° 22 Calcule la medida del ángulo formado por la altura y la bisectriz que parten del vértice A de un triángulo ABC Sabiendo que m ) A 2(m ) C) = 100° a) ° b) 30° c) 40° d) 50° e) 60° 23 Los catetos de un triángulo rectángulo ABC miden AB = 8 u; DOY CORONITA C triangulo notable de 80 y 10 QUIERO SABER LOS CATETOS Y HIPOTENUSA POR FAVORRRRRR 1 Ver respuesta vaniaalbites está esperando tu ayuda Añade tu respuesta y gana puntos JosephGomez16 JosephGomez16 Respuesta Explicación paso a paso Nuevas preguntas de Matemáticas 2Escribir las coordenadas de los pares ordenados D A (1,0) Be CO2) D5,9 5 of EG!De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos Te explicamos cómo encontrar las razones trigonométricas deángulos notablesusando el teorma dePitagorás la altura ylos ángulos deun triánguloequiláteroycalcule exactamente el valor del seno, el coseno yla tangente de30°



Triangulos Notables Recurso Educativo Tiching
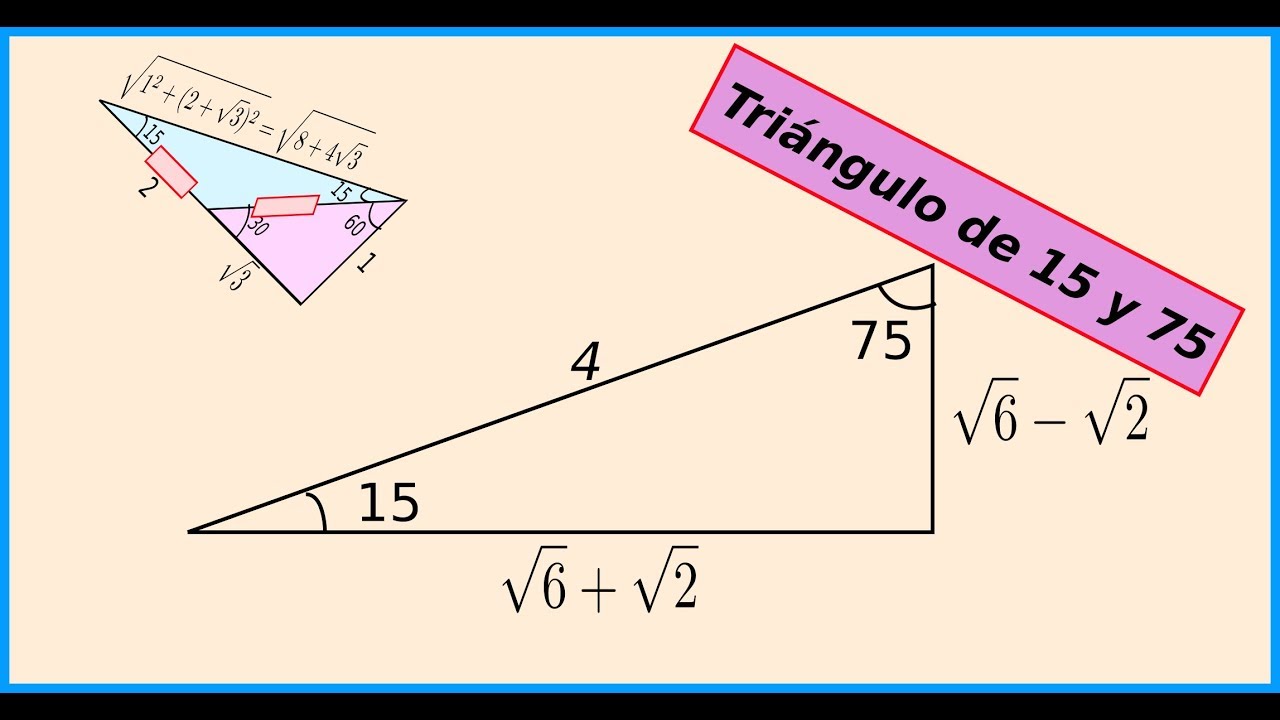



El Triangulo De 15 Y 75 Grados Youtube
Utilizamos tu perfil de LinkedIn y tus datos de actividad para personalizar los anuncios y mostrarte publicidad más relevante Puedes cambiar tus preferencias de publicidad en cualquier momento Próxima SlideShare Cargando en 5 × 1 de 30 ;230 F63 1 15 necesito informacion sobre el triangulo notable de º y 7º feto, #1 doosilver Miembro de bronce Registro Mensajes 1,231 Likes 25 Temas 41 Tal vez, si buscarás en algún libro o poner en internet triángulos notables tengas la respuesta a tu pregunta!




Truco Para Las Razones Trigonometricas De Angulos Notables Matematicascercanas
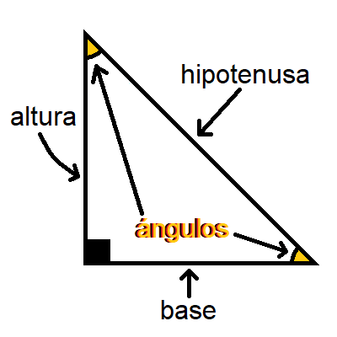



Aekngjyixh2wrm
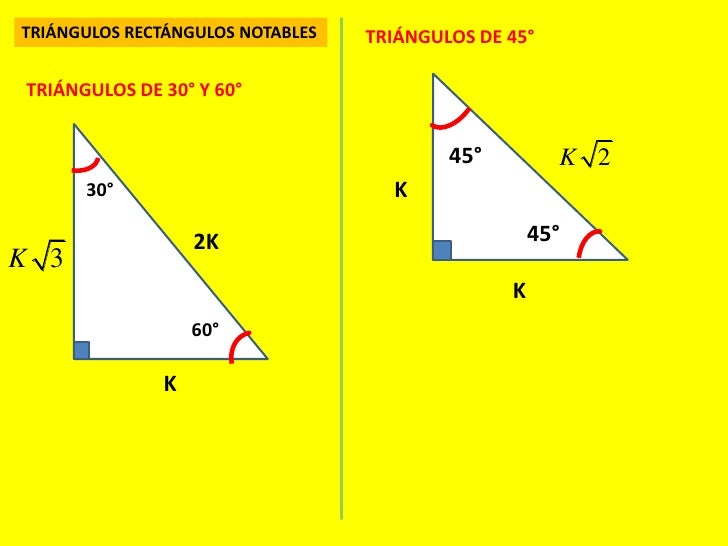
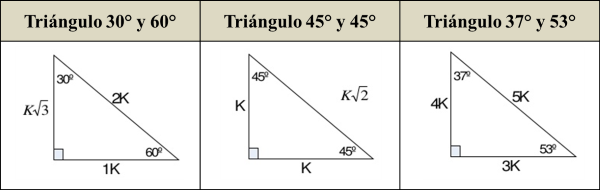
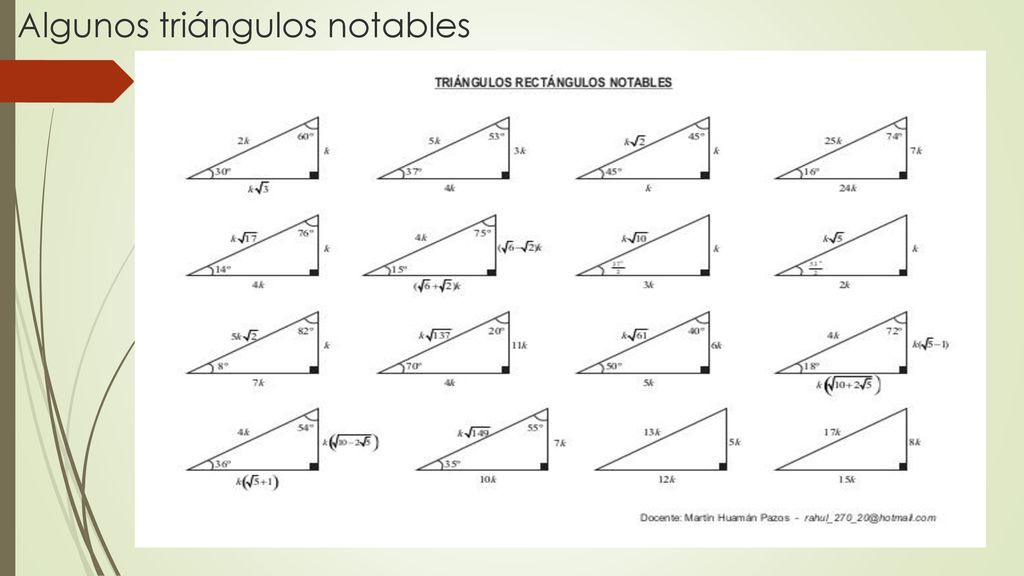
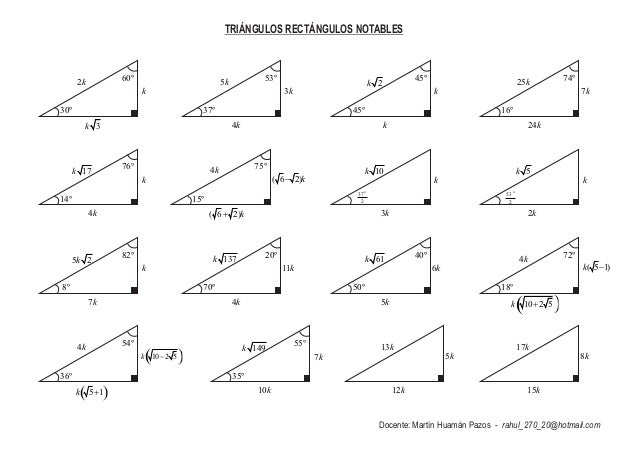
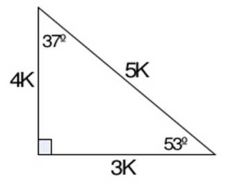
Triangulos rectangulos notables (completo) 1 TRIÁNGULOS RECTÁNGULOS NOTABLES 2k k 3k 30° 60° 5k 3k 4k 37° 53° 2k k k 45° 45° 25k 7k 24k 16° 74° 17k k 4k 14° 76° 4k ( 6 2)k 15° 75° 10k k 3k 37 2 ° 5k k 2k 5 2k k 7k 8° ° 137k 11k 4k 70° ° 61k 6k 5k 50° 40° 4k ( 5 1)k ( )10 2 5k 18° 72° 4k ( )10 2 5k ( )5 1k 36° 54° 149k 7k 10k 35° Luego de haber hecho esto, la mayoría querría usar el Triángulo Rectángulo Notable de 15° y 75° pero seria muy tedioso ya que sus lados contienen raíces proporcionales As í que en vez de eso, expandiremos el lado BC de manera que el lado AB sea igual a la expansión ( lado CP ) Haciendo que se forme un triángulo isósceles, cuyos ángulos iguales medirán la mitad del ángulo Triángulo Notable de 37°/2 y 53°/2 0 más ahora viendo Triángulo Notable de 37°/2 y 53°/2 Jesus Mendez now playing Comas Educación inicial para los niños del colegio Libertad Jesus Mendez




Triangulos Rectangulos Notables Matemath Web




Triangulos Rectangulos Notables
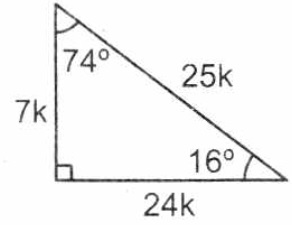
° 1K K√50 8° 7K El triangulo de 8 y 30° K √3 74° 2K 25K 7K 60° 1K El triangulo de 30 y 60 16° 24K El triangulo de 16 y 74 8 √10K K 37°/2 3K El triangulo de 37/2 75° (√6 √2)K 4K √5 K K 15° (√6 √2)K El triangulo de 15 y 75 53°/2 2K El triangulo de 53/2Fue un filósofo y matemático griego considerado el primer matemático puro Contribuyó de manera Podemos caracterizar a un triángulo rectángulo significativa en el avance de la geometría, como notable cuando existe una relación matemática helénica, la aritmética, derivadas conocida entre sus lados Triángulo notable de 16° y 74° Triángulo notable de 15° y 75° Cómo formar un triángulo notable de 15º y 75° Triángulo notable de 14° y 76° Triángulo notable de 37°/2 y 143°/2 Triángulo notable de 53°/2 Cómo formar un triángulo notable de 37°/2 y 53°/2 Triángulo Notable de 45°/2 tags Triangulo Triángulo Rectángulo Triángulos Notables next Razones




Uni Tutors Photos Facebook



Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf
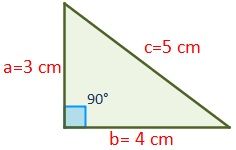
Dibuja un triángulo rectángulo cuyos catetos midan 4 cm y 3 cmDibuja otro triángulo rectángulo en posición de Thales de forma que el cateto mayor mida 8 cm¿Cuánto mide el otro cateto? Triángulo acutangulo de ángulos 135°, 15° y 30° 1 Ver respuesta gstivenxd está esperando tu ayuda Añade tu respuesta y gana puntos luisalexanderpereava luisalexanderpereava Respuesta te ioma Descargar en PDF Vigilar Editar El término burguesía (del francés bourgeoisie)1 se utiliza en las ciencias sociales para designar a la clase media acomodada y a la clase media alta de Para ambos caso el triangulo notables es el triangulo recto Debemos recordar que un triangulo recto o rectángulo es aquel que tiene un angulo de 90° Así mismo, la suma de todos los ángulos internos de un triangulo debe sumar 180° En el primer caso, tenemos los angulo 10 y 80, por lo tanto 10 80 x = 180 x = 180 90



Triangulo Rectangulo




Triangulo Rectangulo Notable De 15 Y 75 Youtube
Triángulo Rectángulo de 30° y 60° Cálculo de un lado desconocido de un triángulo rectángulo conociendo un lado y un ángulo notable Se completa el ángulo que falta en el triángulo rectángulo (en este caso si está el ángulo de 30° el otro ángulo será 60° y viceversa porque ambos suman 90°) Se coloca los lados correspondientemente Ejemplo Del gráfico Calcular E = xLa superficie de una esfera es de 15 m2 Halla la superficie de otra esfera en la que el radio mide el triple Solución S' = 32 15 = 135 m2 7 Solución 224 De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras que posee Más triángulos notables




Triangulos Notables




Triangulos Rectangulos Notables Matemath Web
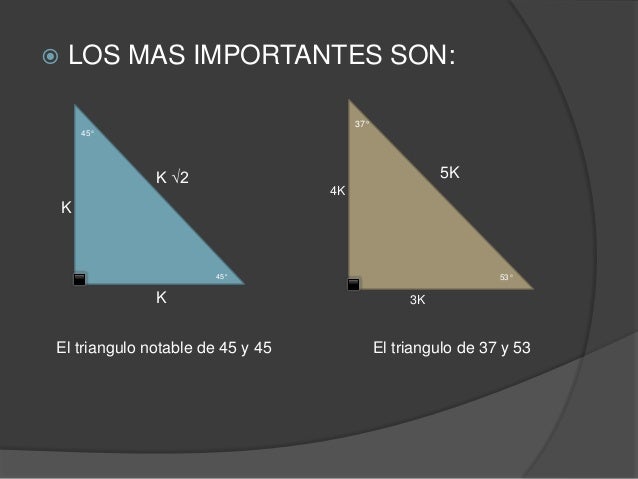
Triángulo notable de 15° y 75° Triángulo notable de 14° y 76° Triángulo notable de 37/2° Triángulo notable de 53/2° Publicado por Unknown en 1613 No hay comentarios Enviar por correo electrónico Escribe un blog Compartir con Twitter Compartir con Facebook Compartir en Inicio Suscribirse a Entradas (Atom) Archivo del blog agosto (1) Datos personales UnknownEl triangulo notable de 45 y 45 El triangulo de 30 y 60 El triangulo de 37 y 53 El triangulo de 37/2 El triangulo de 53/2 El triangulo de 8 y El triangulo de 16 y 74 Publicado por Unknown en 1424 Enviar por correo electrónico Escribe un blog Compartir con Twitter Compartir con Facebook Compartir en Etiquetas Los triangulos notables 126 comentarios Anónimo 15Doosilver, #2 andreb Miembro de bronce Registro Mensajes




Perimetro De Un Triangulo Rectangulo




Razones Trigonometricas De Angulos 14 06 17de Angulos Notables Ejercicios Resueltos 113 C 5 33 D 3 53 E 5 23 Propiedades De Las Razones Trigonometricas Ejercicios
Publishing platform for digital magazines, interactive publications and online catalogs Convert documents to beautiful publications and share them worldwide Title TRIÁNGULOS NOTABLES Y POR APROXIMACIÓN, Author JUSTO GUSTAVO INGA FLORES, Length 2¿Qué es un triángulo Triángulo notable de 15° y 75° Pitágoras rectángulo notable?BC = 15 u Se traza la




Triangulos Rectangulos Notables Matemath Web




Triangulos Notables De 15
Triangulo de Lados 8 , 15 y 17 by silver3samuel3palaciTriángulo rectángulo de 75 y 15 Para más ejercicios resueltos de triángulos notables y de matemática, visita totalmente gratis los siguientes enlaceshttpDe 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras que posee



Deducciones Del Teorema De Pitagoras A Lo Largo De La Historia Como Recurso Didactico En El Proceso De Ensenanza Aprendizaje De La Matematica




Todo Los Triangulos Notables Sus Angulos Medidas
De 15 y 75grados El triángulo notable de 15 y 75 es otro clásico que se suele presentar en repetidas ocasiones dentro de los problemas matemáticos De 16 y 74 grados Este triángulo notable es bastante sencillo de aprender por las proporciones enteras queDos ángulos de un triángulo miden 45° y 60° y otros dos ángulos de otro triángulo miden 75° yScribd es red social de lectura y publicación más importante del mundo




Pin En Libro Logica




Geometria Triangulos Ii Brainly Lat
Podemos caracterizar a un triángulo como notable cuando existe una relación conocida entre sus lados En la mayoría de los casos, las relaci Otros triangulos notables Otros triángulos notables no tan conocidos son El triángulo de 15 y 75 El triángulo de 18 y 72 El triángulo de 36 y 54 Relaciones metricas de un triangulo Relaciones Metricas de un triangulo Relacion Metrica Triángulo Notable de 15° y 75° previous Razones trigonométricas de ángulos notables Parte II next Triángulo Notable de 37°/2 y 53°/2 Triángulo notable de 16° y 74° Triángulo notable de 15° y 75° Podemos caracterizar a un triángulo como notable cuando existe una relación conocida entre sus lados En la mayoría de los casos, las relaciones entre sus lados se limitan a número enteros o número



Razones Trigonometricas Notables De Angulos Agudos En Triangulos Rectangulos Articulo Khan Academy



Resources Aprendoencasa Pe Perueduca Secundaria 5 Semana 14 Pdf S14 Sec 5 Solucion Matematica Dia 3 Pdf




Resolucion De Triangulos Superprof




Todo Los Triangulos Notables Sus Angulos Medidas




Perimetro De Un Triangulo Rectangulo



Unu Edu Pe Cepreunu Pdf Modulos 2geometr C3 8da Trigo iii Pdf



Perimetro De Un Triangulo Rectangulo




Triangulos Notables Reto Y Ejercicios Propuestos Matemovil



2 Supongamos Que Tenemos Una See How To Solve It At Qanda




Triangulos Rectangulos Notables Matemath Web




Triangulos Notables 15 75



1



1




Triangulos Notables Reto Y Ejercicios Propuestos Matemovil




Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos



Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf




Perimetro De Un Triangulo Rectangulo




Los Triangulos Rectangulos Notables Y Sus Respectivos Angulos



Resources Aprendoencasa Pe Perueduca Secundaria 5 Semana 14 Pdf S14 Sec 5 Solucion Matematica Dia 3 Pdf
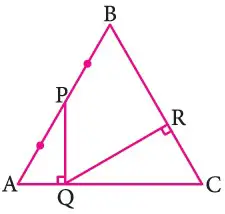



Triangulos Rectangulos Notables Y Pitagoricos Para Tercer Grado




Ppt Matematica 2 Epe Powerpoint Presentation Free Download Id




Triangulos Notables Wikipedia La Enciclopedia Libre



Resources Aprendoencasa Pe Perueduca Secundaria 5 Semana 14 Pdf S14 Sec 5 Solucion Matematica Dia 3 Pdf
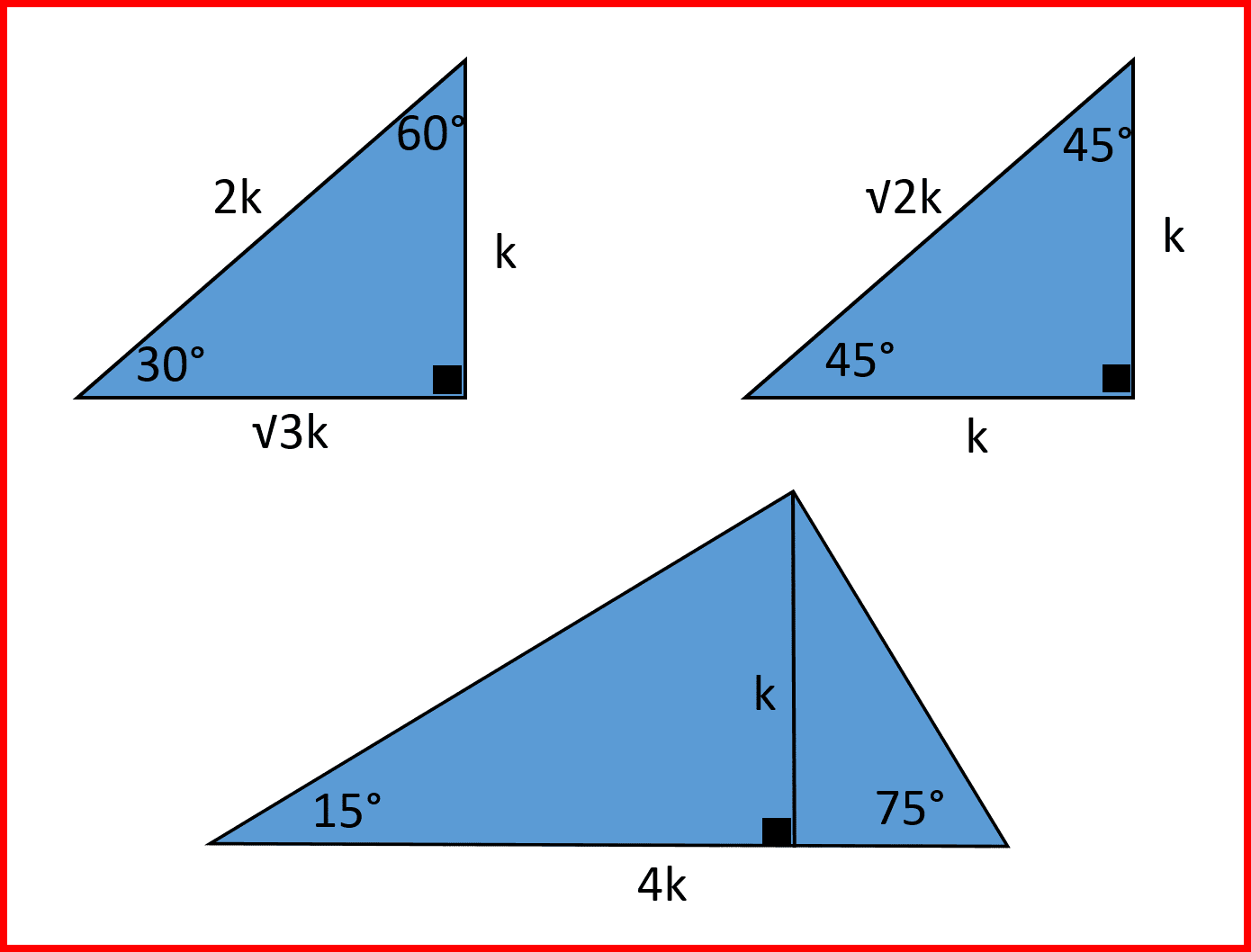



Triangulo Rectangulo Problema 7 Basico
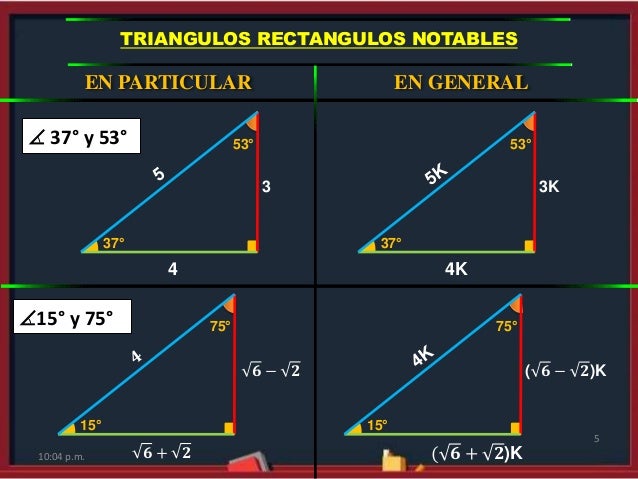



Triangulos Rectangulos Notables




Unidad I Utilicemos Las Razones Trigonometricas Ppt Descargar




Triangulos Rectangulos Notables Matemath Web



Triangulos Notables Pdf Txt




Ejercicios De Triangulos Notables Ayudenme A Resolver Estos Ejercicios Xfa Brainly Lat



Razones Trigonometricas En El Triangulo Rectangulo Ppt Descargar



Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf




Triangulos Notables




En Un Triangulo Rectangulo La Cotangente De Uno De Sus Angulos Agudos Es 0 75 Calcular La Brainly Lat




Hallar A B Triangulos Notables Brainly Lat



Triangulos Notables Reto Y Ejercicios Propuestos Matemovil




248 Sobre Geometrias Sg Sx



Unu Edu Pe Cepreunu Pdf Modulos 2geometr C3 8da Trigo iii Pdf



1



Triangulos Rectangulos Notables Completo



Archivo Triangulo Auxiliar De 75 Y 15 Png Wikipedia La Enciclopedia Libre
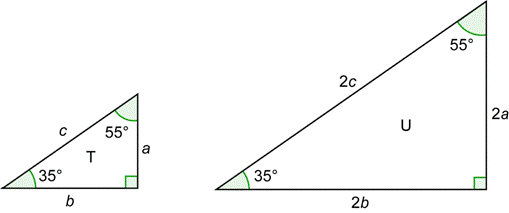



Un Triangulo Rectangulo Tiene Angulos Agudos A Y B Si Y




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulos De 30 Y 60 45 Y 45 37 Y 53 Razones Trigonometricas Notables Ejercicios Res Razones Trigonometricas Ejercicios Resueltos Formulas Matematicas



Razones Trigonometricas Notables De Angulos Agudos En Triangulos Rectangulos Articulo Khan Academy




Pin En Problemas



Triangulo Rectangulo



Triangulos Notables Fhybea




Triangulo Notable De 15 Y 75 6 Youtube




Resolucion De Triangulos Superprof




Calameo Geometria 8



Unidad Vii Geometria Trigonometria Y Series



1




Triangulos Rectangulos Notables Completo



Triangulos Notables By Nicolas Medina By Nicolasmed0123 On Emaze




Truco Para Las Razones Trigonometricas De Angulos Notables Matematicascercanas




Triangulos Rectangulos Notables Matemath Web



Unu Edu Pe Cepreunu Pdf Modulos 2geometr C3 8da Trigo iii Pdf




Problemas De Triangulos Notables Para Tercero De Secundaria 21



Es Static Z Dn Net Files D15 4da1bb799feaa7a35cfc248 Pdf




Todo Los Triangulos Notables Sus Angulos Medidas




Triangulo Notable De 15 Y 75 Profesorajesus Com




Resolucion De Triangulos Oblicuangulos Superprof
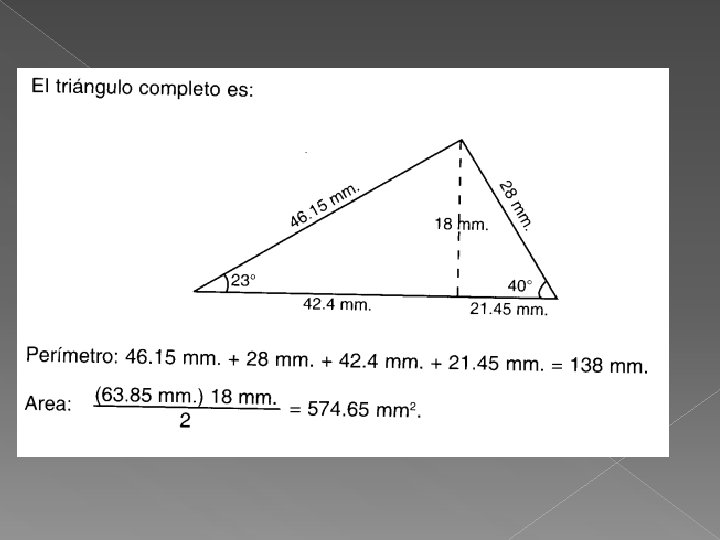



Unidad I Utilicemos Las Razones Trigonometricas Trigonometra Es



Edoc Pub Download Triang Ulos Notables Pdf Free Html




Triangulo Notable De 15º Y 75º Demostracion Youtube




Todo Los Triangulos Notables Sus Angulos Medidas




El Cerebrito Importantes Triangulos Rectangulos Notables Facebook




3 Razones Trigonometricas De 30 60 Y 45 Geometria Plana Con Geogebra Trigonometria I



Triangulos Notable Matematica Para Secundaria
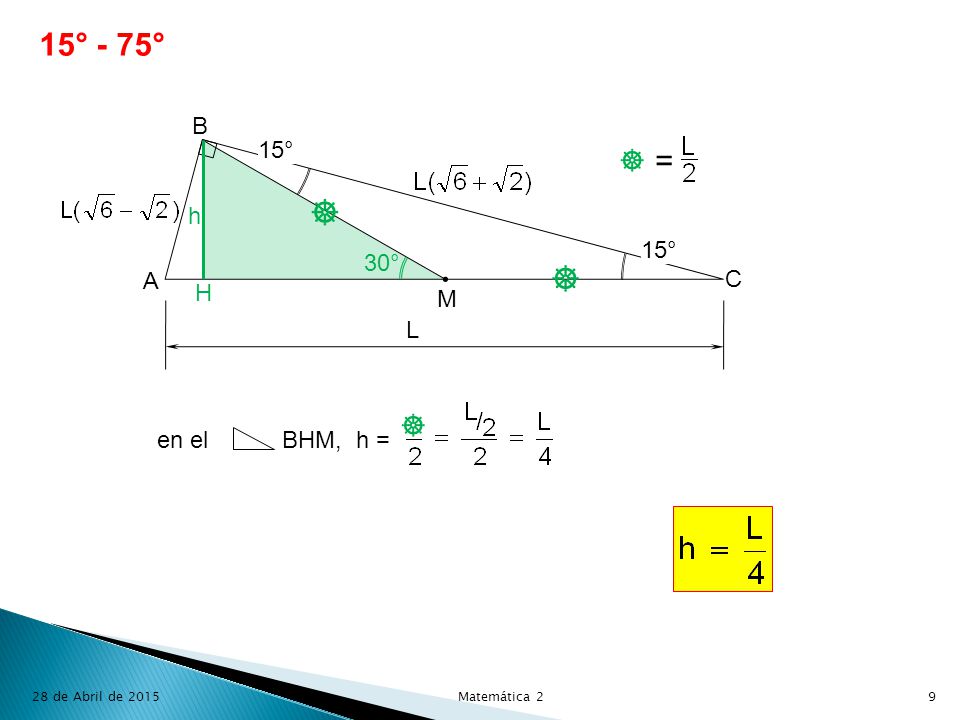



Matematica 2 Epe Area De Ciencias Ma De Abril De Ppt Descargar




Triangulos Notables Ejercicios Resueltos Pdf




Razones Trigonometricas En Triangulos Rectangulos Video Khan Academy




Triangulos Rectangulos Notables Matemath Web




Resolucion De Triangulos Superprof
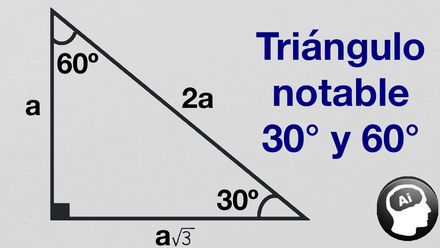



Triangulos By Romario Kaliman On Emaze



Http Www Itsmante Edu Mx Wp Content Uploads 17 11 Cuadernillo De Trigonometria Pdf
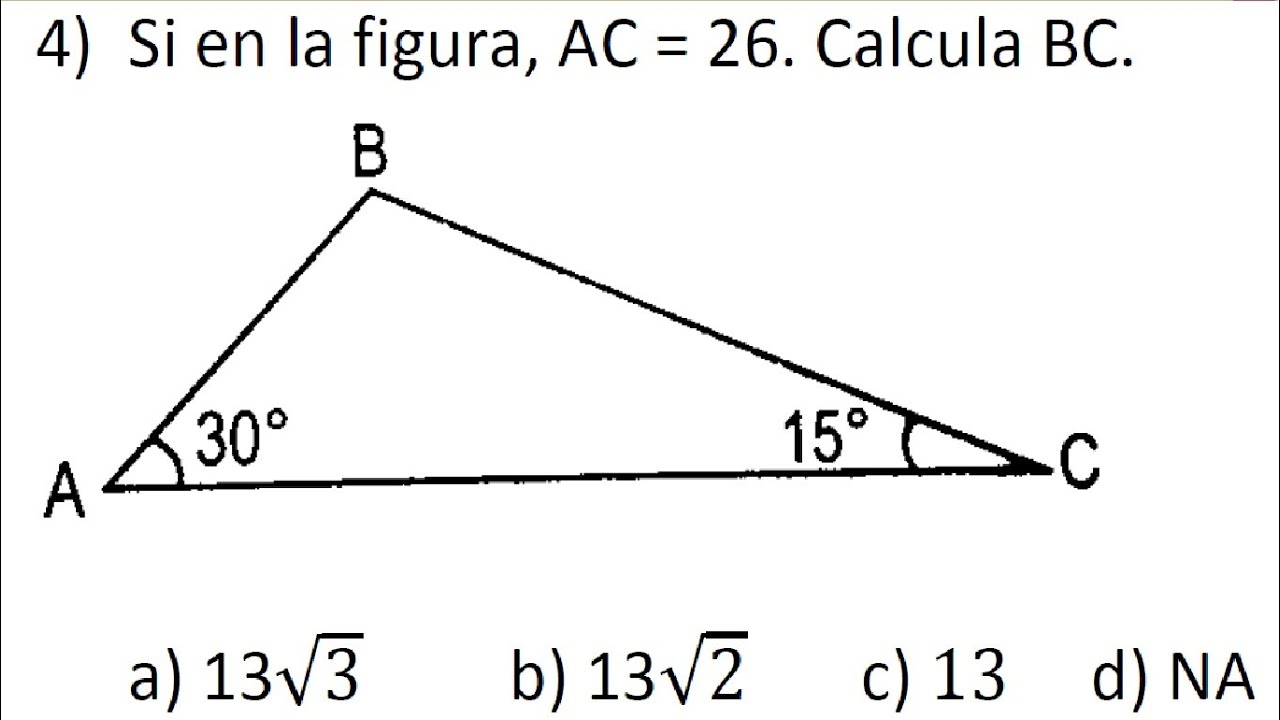



Triangulo Rectangulo Notable 15 Y 75 Youtube




Todo Los Triangulos Notables Sus Angulos Medidas



Triangulos Notables




Resolucion De Triangulos Superprof


