問われているのは、①または②になる確率なので、言いかえれば③にならない確率である。 つまり余事象で解きましょう。 ③になる確率を求めます。 本のくじから2本を引く場合の数は C 2 =190(通り) 17本のはずれくじから2本をひく場合の数は、 17 C 2 =136(通り) よって、2本ともはずれを引く確率は 136 190 = 68 95 136 190 = 68 95くじで当たる確率を求めるときに,「当たりかはずれかどちらかだから,当たる確率は2分の1」などと雑な議論をしてはいけない. 右図1のように,5本のくじの中に当たりくじが2本入っているときに,1本引いて当たる確率は,次のように求められる. くじの出方の 全体の場合の数 は N =5 当たりくじが出る 場合の数 は n =2 どのくじの出方も「 同様に確からしい例題 次の確率を求めよ。 (1) 3つのさいころを同時に投げるとき,目の和が5になる確率。 (2) HAKATAの6文字を1列に並べるとき,母音と子音が交互に並ぶ確率。 ①起こりうる全ての場合の数の集合をU、確率を求めたい場合の数の集合をAとすると Aの起こる確率 は次のように表せます。 ②確率を求めるにあたって、場合の数を数えるとき、抜けが無いようにするため

確率 スタディーx
確率 の 問題
確率 の 問題-確率 基本的な確率の問題練習プリントです。 確率とは ある事柄の起こりうることが期待される程度を表す数 サイコロを投げたとき、3が出る確率は6分の1になります。 *サイコロに何か細工をしない限り、サイコロのどの目の出方も同じに 16年4月93 場合の数と確率の基本問題 問題1 1から4までの4枚のカードを使って4けたの数を作ります。 何通りの数ができますか。 → 解答 問題2 A、B、C、D、E、Fの6チームが野球をします。 各チーム1回ずつ対戦する場合、全部で何試合することになるでしょう。




数学 場合の数 確率 分野別標準問題精講 森谷慎司 本 通販 Amazon
神奈川県 Aliceさんからの問題。これは難問! ・『ビュッフォンの針』 前題と同じタイプの問題です。 広島県、東京都からの解答を掲載。 ・『球面上の鋭角三角形の確率』 神奈川県 @JJJJJJ さんからの問題です。高校生以上向き。練習問題1 1から10まで、1つずつ整数が書かれたカードが10枚ある。 この中からカードを2枚続けて引く。 (1) 1枚目に引いたカードを戻して、よく切った後に2枚目のカードを引く。 このとき、少なくとも1枚は3の倍数である確率はいくらか。 (2) 1枚目に引い26 rækker練習問題 練習問題+解答 組合せの総数 n C r が整数であることの証明確率 例題(8)
高校数学 解説動画 数学a 場合の数と確率 確率の基本① さて今回は基本編に突入します(`・ω・´) まずは、さいころを使った問題と、人や数字を並べる問 記事を読む 高校数学 解説動画 数学a 円順列 次は円順列です。一方 確率の問題は、「これ1つで大丈夫! 」という解法が存在しない のだ。 いつも同じ公式に従って計算するわけではなく、場合によって計算方法は様々だ。 したがって、 問題を見たときに解法が一瞬では思いつけない 。 次の2つの例題を見れば分かるだろう。 <例題1>関数 を微分せよ。 <例題2>サイコロを2つ同時に振るとき、出た目の積が6の倍数になる確率の問題は、 単に『確率』を求める公式を覚えているだけでは解けない 場合があります。 何故なら よって、 『組み合わせ数』を求める公式と、『確率』を求める公式の両方を覚えておく 必要があります。 更に嫌になることを記載しますが、『組み合わせ数』を求める公式と、『確率』を求める公式は、それぞれ 4種類ずつの計8つ あります。 ただ、必ず覚え
確率論の基礎的内容を第1 章で扱い, 2 章以降でブラウン運動の基礎的内容, 電気回路と確率論に関連 する話題などを扱っている ファイナンスではどのように確率論が用いられているかも2 章で扱って099 ×001 = (病気かつ検査が正しい+病気でないかつ検査が間違う) P ( A ∩ B) = ×099 = P (A\cap B)=\times 099= P (A∩B)= ×099 = よって,




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ
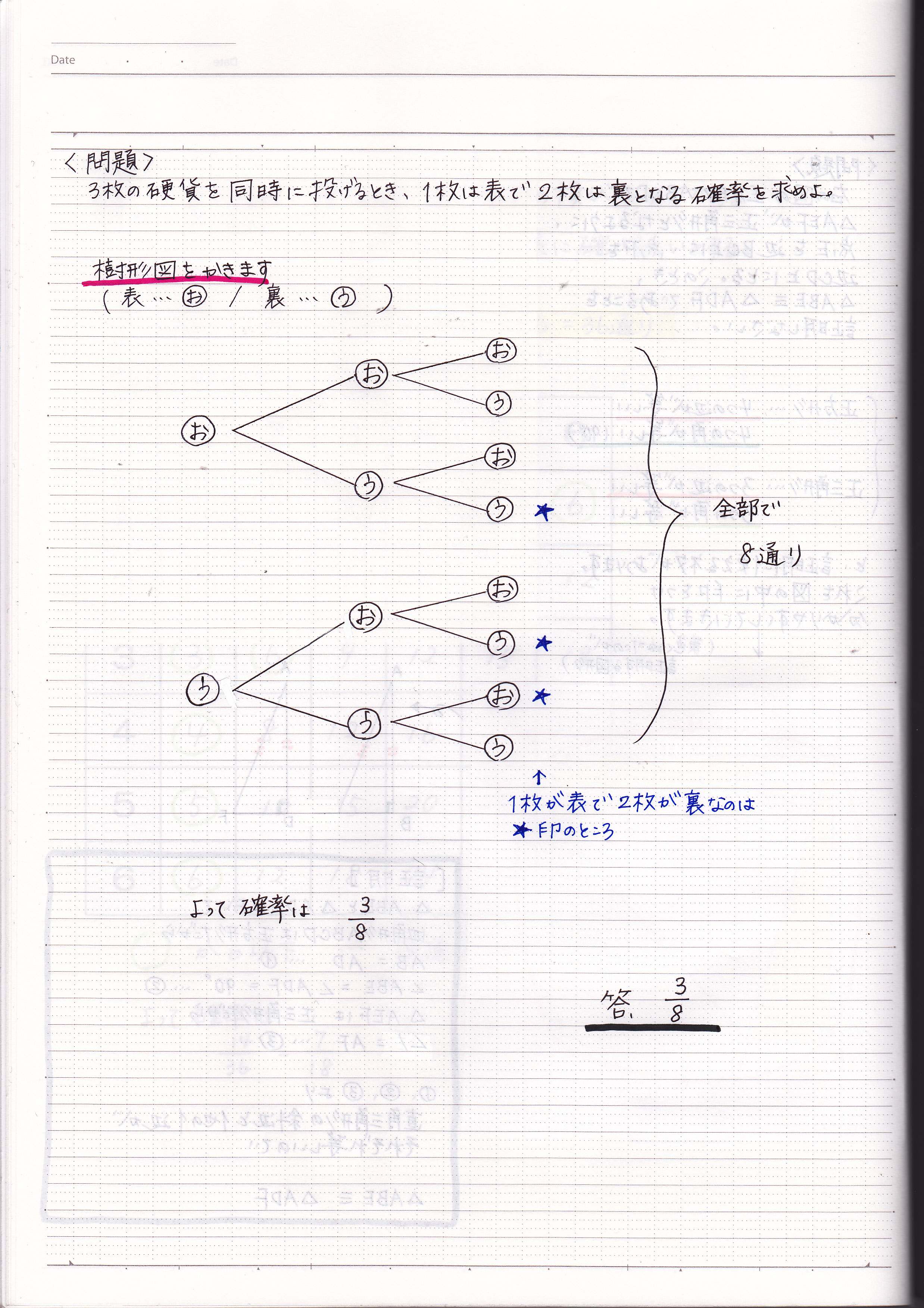



確率の問題の解き方 コインの表と裏 2 現役塾講師のわかりやすい中学数学の解き方
9 確率と期待値 練習問題(9 確率と期待値) ジョーカーを抜いた52枚のトランプから1枚をランダムに取り出すとき、ハートのエースが出る確率を求めよ。 ランダムに取り出すとき、どのカードが出るかは同様に確からしくなります。 通りの取り出し方に対して、ハートのエースが出る事象は1通りしかありません。 したがって、答えは になります。 エースから場合の数 ③練習問題 確率 確率 ①基礎確率 Aが起こる確率 = Aが起こる場合の数 / 全ての場合の数 ・・・ということなので、 場合の数がキチンと理解できていれば、とてもカンタンです! 「 3 P 2 」とか「 3 C 2 」が 分からない方はこちら! ⇒ 場合の数



中学数学単元別 確率 数学 中学校 教材 問題集 7 学林舎 通販 Yahoo ショッピング




中学数学の確率の問題の解き方 コイン サイコロ くじ カード 数学fun
099 ×3 第1章 1~6章の問題と解(確率) 11 基礎概念 p4 問1 赤球2個,白球1個の入った箱から次のようにして2個の球を取り 出すとき,赤球2個が取り出される確率を次の各々の場合に求めよ。問7 確率変数x は正規分布n(3;22) に従うとする.このとき (1) 正規分布表を用いて確率 P (2 ≦ X ≦ 3) を求めよ. (2) P (3 a ≦ X ≦ 3 a ) ≒ 09 となるような a の値を求めよ.( 15 点)



条件付き確率 京極一樹の数学塾
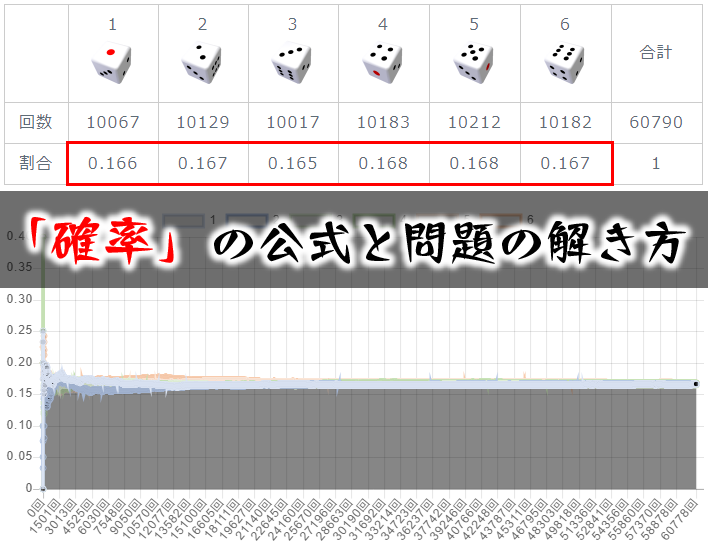



確率の公式と基本的な問題の解き方 数学fun
第2学年 6 確率 知識・技能の習得を図る問題 年 組 号氏名 練習問題① 1 次の(1),(2)の各問いに答えなさい。 (1) 投げたとき,表になる確率が である硬貨があります。順に6654とでる確率は1/6の4乗=1/1296です。 5が何回目に出たのかで4通り、4が何回目に出たのかで3通り、 全部で4×3=12通りあります。 5466 5646 5664 など全12通り そのいずれも、同じ確率なので、1/1296 ×知識・技能の習得を図る問題 年 組 号氏名 練習問題① 1 次の(1),(2)の各問いに答えなさい。 (1) 投げたとき,表になる確率が である硬貨があります。この硬貨を投げるとき,どのようなこと がいえますか。




中2数学 確率問題の解き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
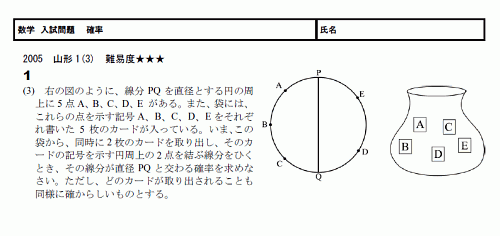



確率 スタディーx
目次問題さあ、解いてみよう!正解解説「起こらない」確率車が「通らない」確率補足:ポアソン過程まとめ参考140字以内の問題文 問題 ある道路では、30分以内に車が通る確率は95%である。 では、10分以内に車が通る確率は?Amazonで上野 健爾, 高専の数学教材研究会の確率統計問題集 (高専テキストシリーズ)。アマゾンならポイント還元本が多数。上野 健爾, 高専の数学教材研究会作品ほか、お急ぎ便対象商品は当日お届けも可能。また確率統計問題集 (高専テキストシリーズ)もアマゾン配送商品なら通常配送無料。分割払い ②練習問題 場合の数 場合の数 ①基礎;
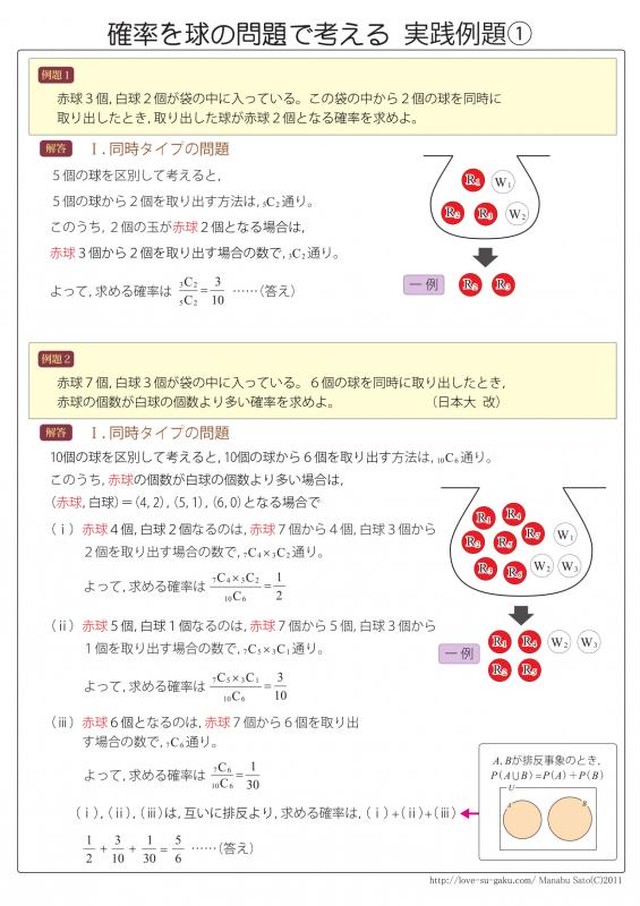



数学a 確率を球に関する問題で考えるチャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru




確率がよく分かる参考書のおすすめ人気ランキング10選 数学の苦手分野克服に Mybest
ちょっと面白い確率の問題 直感は当てにならない? 21 2/06 数学の欠片 前の記事『 数学者も悩んだ確率の話 モンティー・ホール問題を解説してみた 』で、モンティー・ホール問題という直感に反するような確率の問題を紹介しました。 他にも、不思議で面白い確率の問題を紹介しましょう。 直感と違う結果が出て、戸惑うかもしれませ4割合 分割払い 分割払い ①例題;P ( A) = ×




中学数学 さいころ2個の確率問題をパターン別に解説 数スタ




高校数学 確率 玉が登場する確率問題の解き方 数学の面白いこと 役に立つことをまとめたサイト
秘書問題の最適戦略 k k k 人目まで無条件で断り, k 1 k1 k 1 人目以降で「今までで一番いい人」が現れたら交際する,というタイプの戦略(戦略 S k S_k S k と呼ぶ)を取ることにします。 直感的に自然な戦略です。 k k k をどのように定めればよいかを考えます。確率問題全般 疑問点のお問い合わせやご注文などは、admin@KKyogokucomへお願いします。 ただし、恐れ入りますが、 御注文・お問い合わせの手順にしたがってお願い致しします。 見たことのない問題を限りなく減らすために: 東大、京大、慶応大/医、順天堂大/医などを受確率の考え方と、いろいろなタイプの確率の問題について学習します。 確率・サイコロ 確率・コイン・くじ 確率・玉・じゃんけん 確率 確率 確率 確率 確率




条件付き確率の公式や求め方とは 問題を使ってわかりやすく解説 東大医学部生の相談室




よく出る 確率の問題 あたりくじ インターネット家庭教師のアスミラ
B君が当たる確率を求めよ。 A君、B君ともに当たる確率を求めよ。 A,B2つのサイコロを同時に投げる。 Aの目をx、Bの目をyとして座標上に点P (x,y)を取る。 点Pがy=x2のグラフ上にある確率を求めよ。 右図で点S (1,7),点T (8,5)である。 点Pが SOTの内部 (図の影をつけた部分)にある確率を求めよこの演習問題集では,断らなければ以下の設定が与えられていると仮定し,また以下の 記号を断りなく使う. 設定 • 確率空間(Ω,F,P) が与えられているとする. • X n, Y n, Z n, n ∈ N, は((Ω,F,P)上の)確率変数列,X, Y, Z は((Ω,F,P)上 の)確率変数とする.001 = P (A)=\times \times 001= P (A) = ×
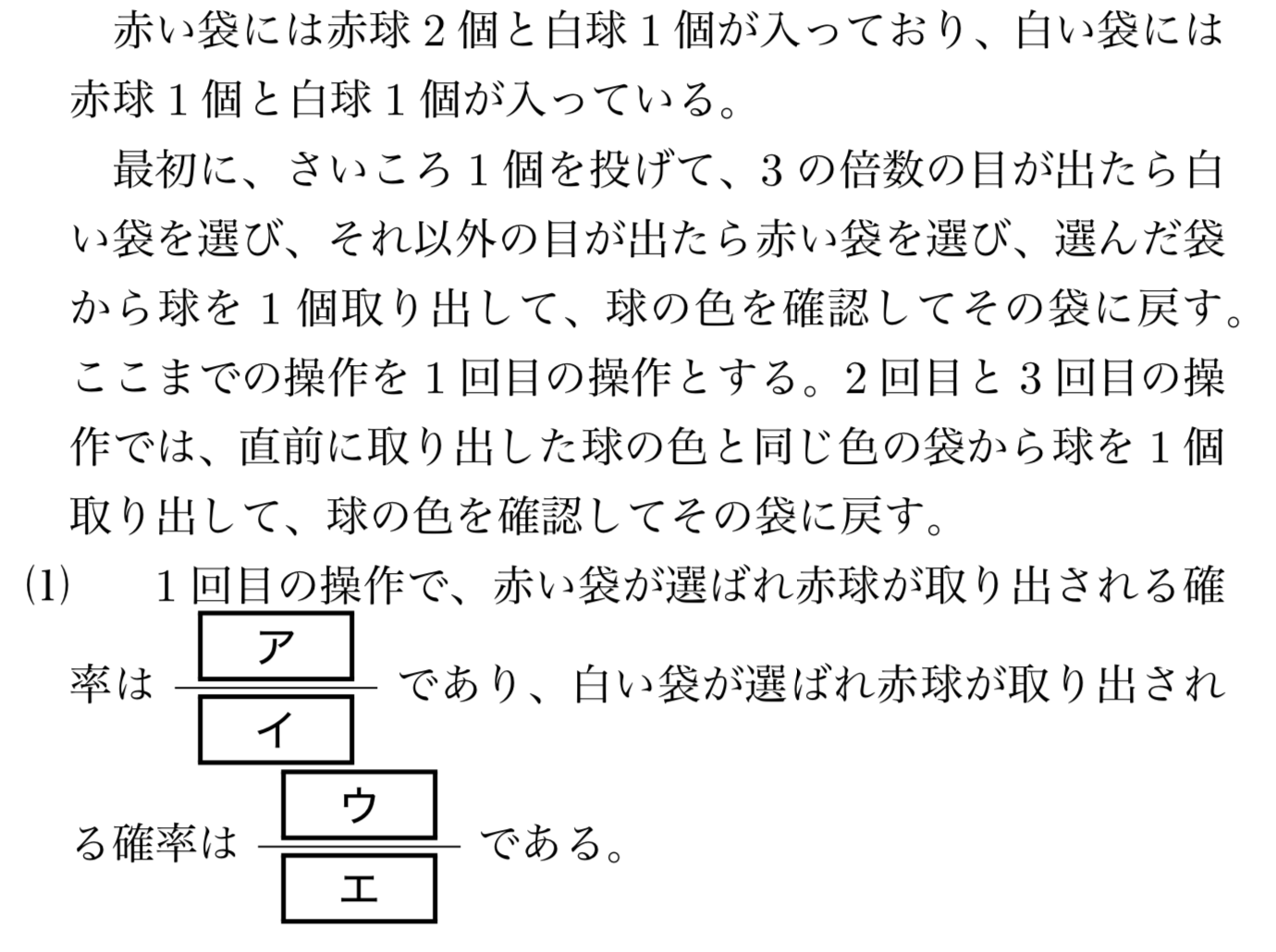



19年センター試験 共通テスト 数学 Aの確率漸化式に似た問題の解答 解説 東大医学部生の相談室




確率統計問題集の通販 上野 健爾 高専の数学教材研究会 紙の本 Honto本の通販ストア
3割合 団体割引 割合 団体割引 ①例題;確率過程とその応用:問題略解 1 「確率過程とその応用」問題解答 逆瀬川浩孝 1 確率過程 練習11 X(t) を来年元旦から数えてt 日目の西早稲田キャンパスでの火災発生件数としたと き、X(t) のサンプルパスを描きなさい。 略解:X(0) = 0、火災発生時点で1 ずつ増加する階段関数。確率 タイトル 出題 問題閲覧 今は公開中 1確率の本質① 《京都大12年文系》 問題を見る 公開中




中学2年生 数学 確率 資料の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




大学入試10日で極める場合の数と確率 理系のための分野別問題集 数研出版編集部 本 通販 Amazon
確率, そうでない企業からの申し込みは % の確率で審査を通る この銀行の審査を通過した企業が優良 である確率を求めよ 練習問題22 ある試験では, 問題が5 問, 解答が4 択になっている 全ての問題にランダムに解答したと き, 2 問正解となる確率を求めよ




条件付き確率の公式とは 不良品の問題など4選もわかりやすく解説します 遊ぶ数学
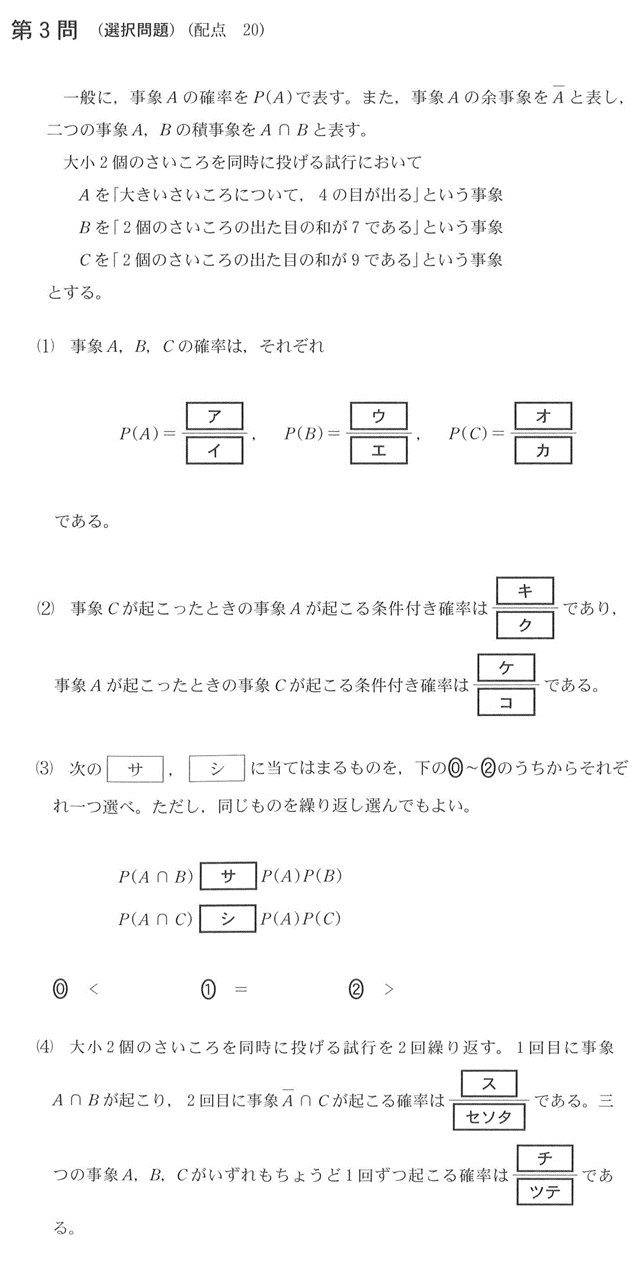



センター試験 場合の数と確率 の必勝テクニック 第3回 応用編 高校生3分ニュース 進研ゼミ高校講座




高校数学無料問題集 数a 第1章 場合の数と確率 確率の計算 桝 ます Note
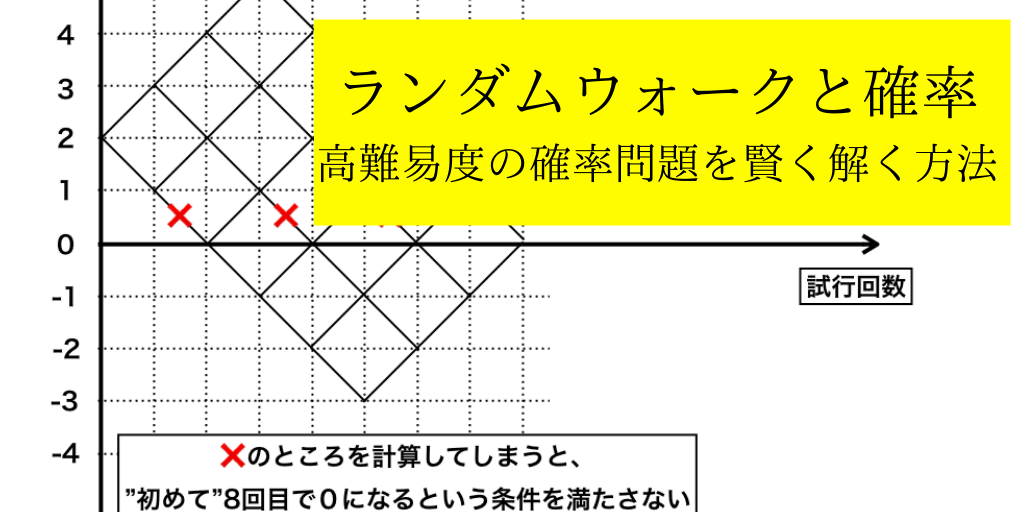



ランダムウォーク 酔歩 の意味と確率の問題の解法を分かりやすく解説



新確率統計問題集 大日本図書
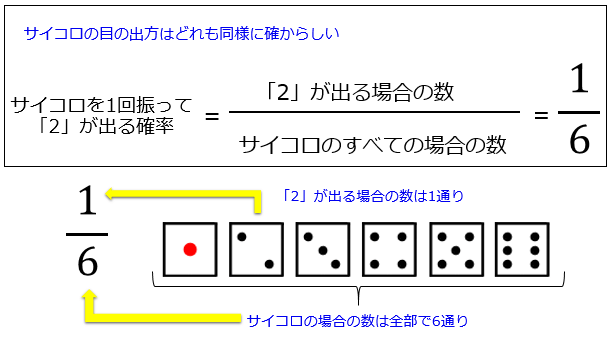



確率計算の公式から 確率の求め方の苦手ポイント 同様に確からしい を武器に変える記事 アタリマエ




数a 確率 写真の 1 が分かりません Clear




数学 場合の数 確率 分野別標準問題精講 森谷慎司 本 通販 Amazon




確率 コイン サイコロ くじ 数字カード 計算ドリル 問題集 数学fun




中学2年数学 確率 場合の数を求める問題の解き方 数学の面白いこと 役に立つことをまとめたサイト




高校数学a じゃんけんの確率 N人のじゃんけん 受験の月




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ



余事象とは 記号 意味 公式や 余事象の確率の問題 受験辞典




確率 スタディーx




中学2年生 数学 確率 資料の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学 確率の問題を攻略できる5つのコツ Qikeru 学びを楽しくわかりやすく




場合の数と確率 の問題のわからないを5分で解決 映像授業のtry It トライイット



確率問題全般 京極一樹の数学塾




高校数学 確率問題 苦手単元克服 センター試験 Spi 大学受験 公務員試験 就職試験対応 For Android Apk Download




確率 確率の問題の解き方 中学数学 定期テスト対策サイト




1講 事象と確率 2節 確率 問題集 高校数学a




無料 中2数学 標準問題 解答プリント 235 確率3 求め方




確率 スタディーx




確率の問題なのですが 途中まではコンビネーションを使って解けたのですが そのあとの2 Clear




中2数学 確率の求め方 練習編 映像授業のtry It トライイット




確率 Probability Japaneseclass Jp



Q Tbn And9gcttihqoxpymu 409s Szdq5woevcnjzbng013exk9dp Rhmmohm Usqp Cau




Spi 数学 対策問題 確率 組み合わせ しかくのいろは




中学数学 確率 コインを使った確率の問題を攻略しよう Youtube




高校受験対策 数学 確率6の問題 動画 19ch



大学入試数学の問題



確率とは 公式 問題での計算式の立て方と解き方 受験辞典




問題14 全部 確率分布ノート 解説動画 チャート式の数研出版




確率13 原因の確率の導入例1 怜悧玲瓏 高校数学を天空から俯瞰する




条件付き確率の問題です 大学入試数学問題の解説 解答




確率の問題 まとめ Togetter



数学i Aチェック リピート 第8章 3条件つき確率 乗法定理 3 原因の確率 Pukiwiki



2016年前期東大入試理系数学 第2問 ほのぼの数学頑張ろう




中学2年生 数学 確率 資料の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
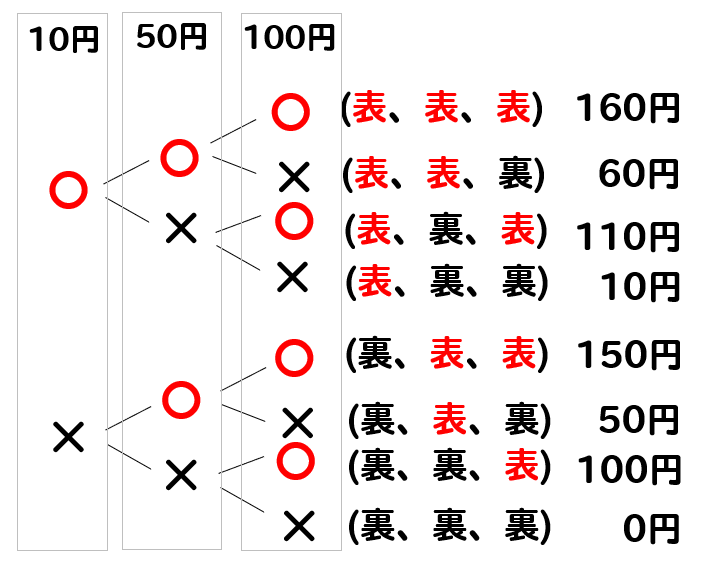



確率 硬貨を同時に投げるときの問題をパターンごとに解説 数スタ




中学数学 確率 二つのサイコロが出てくる確率の問題を攻略 Youtube



確率数列の問題 京極一樹の数学塾




共通テスト確率問題実行器 Iphoneアプリ Applion




確率と場合分け 17年度岐阜県 高校入試 数学 良問 難問




3分でわかる 確率の問題を解くための6つの基礎知識 合格サプリ




高校生 数学a 東京書籍 1章3節 いろいろな確率 節末問題 赤城 ᐡᐤᐡ




大学入試 苦手対策 場合の数 確率 に強くなる問題集 大学入試苦手対策 シリーズ 4 箕輪浩嗣 本 通販 Amazon
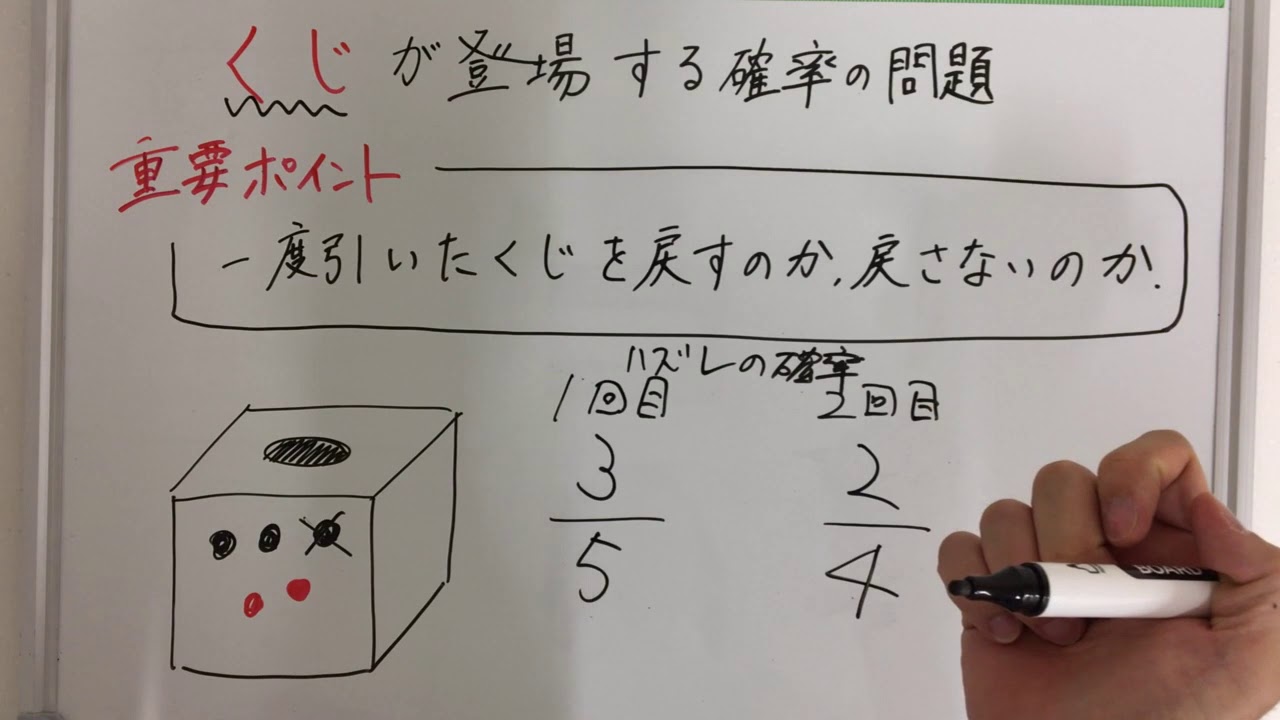



中学数学 確率 くじを使った確率の問題を攻略しよう Youtube



1




2019年 東大数学 文系第3問 確率 多角形グルグル 道順 中学受験で解ける 東大に文理両方で合格した男が綴る 受験の戦略
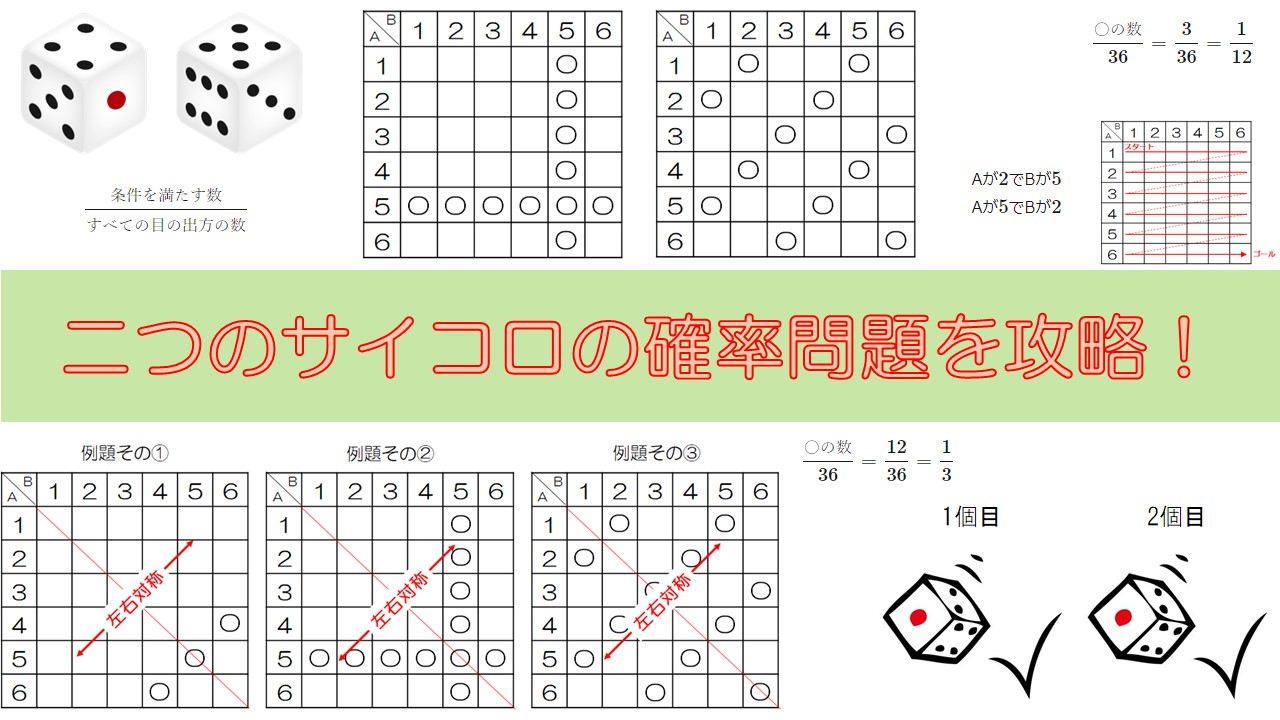



中学2年数学 確率 二つのサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト




中学2年数学 確率 カードが登場する確率の問題の解き方 数学の面白いこと 役に立つことをまとめたサイト




数学a 確率 の問題を教えて下さい 画像の問題 1 なのですが a Okwave




黒木玄 Gen Kuroki 検査陽性のときに 実際に病気有りの確率 を求める問題は高校レベルの数学の問題です 大学入試でも出題されています 問題を解くためにはベイズの定理も統計学も必要ない 2 2の分割表を書くだけでよい 神戸薬科大学入試問題17




高校数学無料問題集 数a 第1章 場合の数と確率 条件付き確率 桝 ます Note




1講 事象と確率 2節 確率 問題集 高校数学a




高校数学 確率問題 苦手単元克服 センター試験 Spi 大学受験 公務員試験 就職試験対応 Fur Android Apk Herunterladen



数学i Aチェック リピート 第8章 1確率とその基本性質 1 同様に確からしい Pukiwiki




確率問題に潜む定積分 10年 京大 理系 数学日和



高校数学 問題検索 数学a 場合の数と確率 確率の基礎 数学
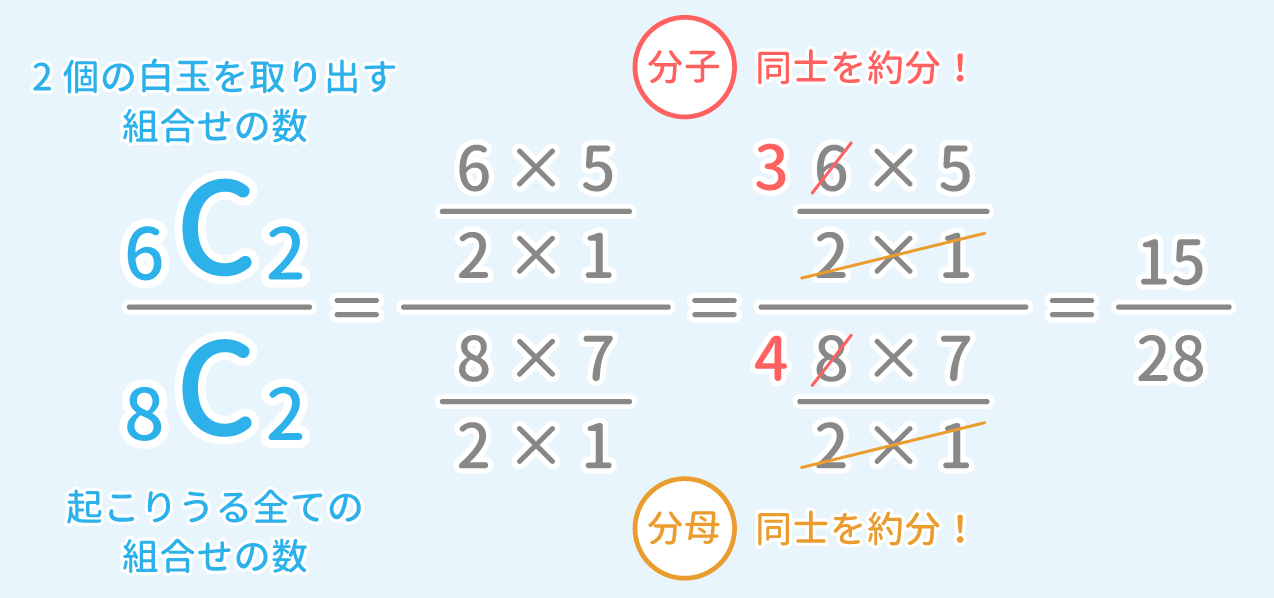



Spi 確率 最速解法 例題 Study Pro Spi



分野別 標準問題精講 場合の数 確率 の難易度 問題数 使い方 オンライン講師ブログ
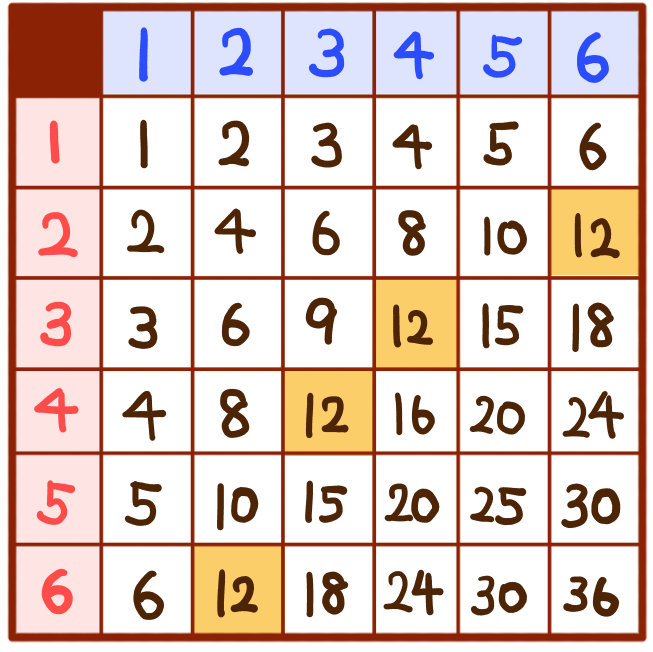



サイコロの確率の練習問題 高校入試 中学数学 を難問まで難易度別に解説 坂田先生のブログ オンライン家庭教師の数学講師




確率22 鯉のぼり問題 怜悧玲瓏 高校数学を天空から俯瞰する




中学2年数学 確率 確率の求め方 たった1つの公式ですべてわかる 数学の面白いこと 役に立つことをまとめたサイト




数学確率 高校入試問題で添付の確率の問題がわかりません 宜しくお願 高校受験 教えて Goo




大学入試 苦手対策 データの分析 確率分布 統計的な推測 に強くなる問題集 旺文社
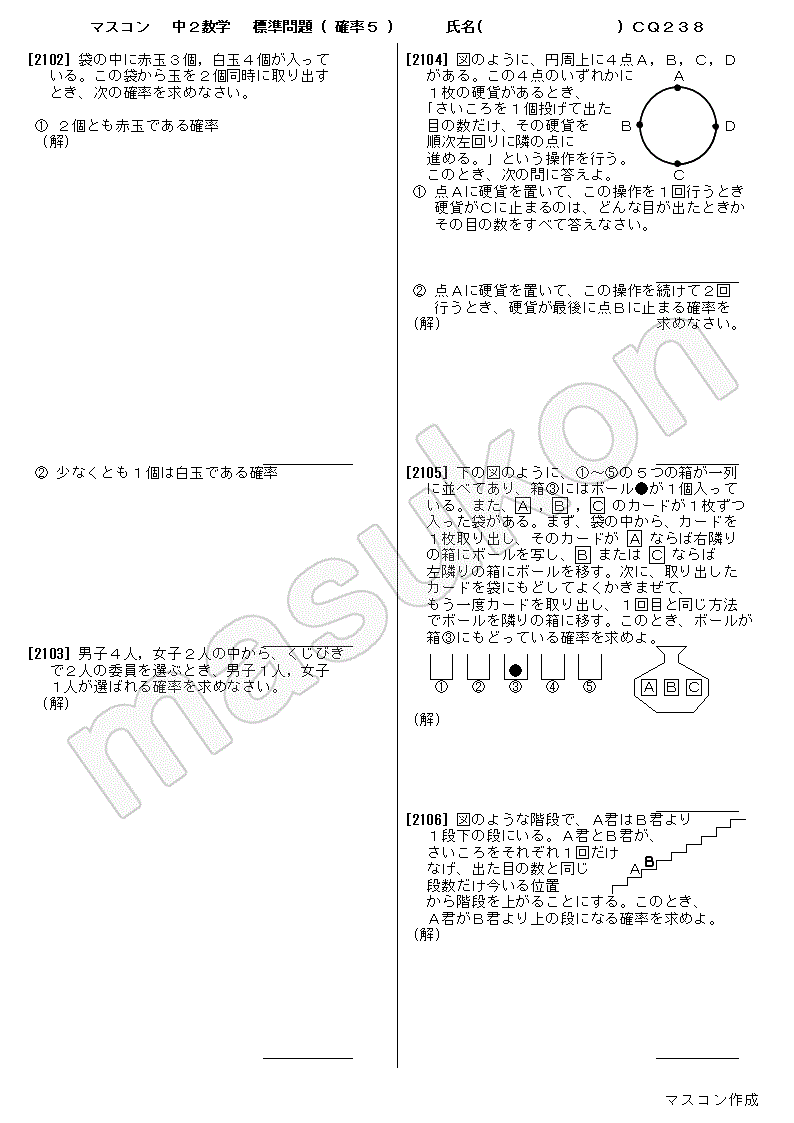



中2数学の標準問題プリント 問題と解答




確率の基本的な問題 2018年度前期日程奈良女子大学理学部入試問題 身勝手な主張



確率問題全般 京極一樹の数学塾




確率の問題を間違えてしまう5つの原因と求め方とは 高校生向け受験応援メディア 受験のミカタ



Spi M54e217p7lcis9d Com Category E7 Ba E7 8e 87




面白い数学の問題 トランプがダイヤである確率 早稲田大学の入試問題が中学生でも解ける そらの暇つぶしch




無料 中2数学 発展問題 解答プリント 236 確率4 求め方2




中学2年生 数学 確率 資料の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学



確率問題として有名なモンティ ホール問題のよく分かる解説 35歳オジサンの婚活ドタバタ奮闘記



Q Tbn And9gcrqye5zqhk2cefu4ah2q54smce7 Fcevnndil3waz2fdfvgsw7h Usqp Cau



Spi M54e217p7lcis9d Com Kakuritu Q3




場合の数 確率の攻略 基礎編



さいころ 球 カードの確率の問題 Of 京極一樹の数学塾会員頁




19年 東京都 高校入試 数学 確率の問題 数樂管理人のブログ




メルカリ 数学a 場合の数と確率 問題集及び解答編 参考書 350 中古や未使用のフリマ




無料 中2数学 テスト対策 問題プリント 219 場合の数と確率2 確率1




確率の問題の解き方 プレゼントを贈り合う 現役塾講師のわかりやすい中学数学の解き方



1


